 Научные и курсовые работы |
Главная
Исторические личности
Военная кафедра
Ботаника и сельское хозяйство
Бухгалтерский учет и аудит
Валютные отношения
Ветеринария
География
Геодезия
Геология
Геополитика
Государство и право
Гражданское право и процесс
Естествознанию
Журналистика
Зарубежная литература
Зоология
Инвестиции
Информатика
История техники
Кибернетика
Коммуникация и связь
Косметология
Кредитование
Криминалистика
Криминология
Кулинария
Культурология
Логика
Логистика
Маркетинг
Наука и техника Карта сайта
Курсовая работа: Статистический анализ деятельности предприятия
Курсовая работа: Статистический анализ деятельности предприятия
ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра ИнОУП
Курсовая работа
«Статистический анализ деятельности предприятия»
по дисциплине: «Статистические основы документационного обеспечения»
Пояснительная записка
ПГУ 2.032001.117 ПЗ
Выполнила: ст-ка гр.06ВД2
Е.П. Смурыгина
Принял: ассистент
Ю.Ю. Фионова
Введение
Задачи математической статистики
Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении методами теории вероятностей статистических данных — результатов наблюдений.
Первая задача математической статистики — указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов.
Вторая задача математической статистики — разработать методы анализа статистических данных в зависимости от целей исследования. Сюда относятся:
а) оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости случайной величины от одной или нескольких случайных величин и др.;
б) проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен.
Современная математическая статистика разрабатывает способы определения числа необходимых испытаний до начала исследования (планирование эксперимента), в ходе исследования (последовательный анализ) и решает многие другие задачи. Современную математическую статистику определяют как науку о принятии решений в условиях неопределенности.
Итак, задача математической статистики состоит в созадании методов сбора и обработки статистических данных для получения научных и практических выводов.
Способы отбора
Принципиально эти способы можно подразделить на два вида:
1 Отбор, не требующий расчленения генеральной совокупности на части:
1.1 простой случайный бесповторный отбор;
1.2 б) простой случайный повторный отбор.
2 Отбор, при котором генеральная совокупность разбивается на части:
2.1 типический отбор;
2.2 механический отбор;
2.3 серийный отбор.
Простым случайным называют такой отбор, при котором объекты извлекают по одному из всей генеральной совокупности. Осуществить простой отбор можно различнымн способами. Например, для извлечения п объектов из генеральной совокупности объема N поступают так: выписывают номера от 1 до N на карточках, которые тщательно перемешивают, и наугад вынимают одну карточку; объект, имеющий одинаковый номер с извлеченной карточкой, подвергают обследованию; затем карточку возвращают в пачку и процесс повторяют, т. е. карточки перемешивают, наугад вынимают одну из них и т. д. Так поступают п раз; в итоге получают простую случайную повторную выборку объема п.
Если извлеченные карточки не возвращать в пачку, то выборка является простой случайной бесповторной.
При большом объеме генеральной совокупности описанный процесс оказывается очень трудоемким. В этом случае пользуются готовыми таблицами«случайных чисел», в которых числа расположены в случайном порядке. Для того чтобы отобрать, например, 50 объектов из пронумерованной генеральной совокупности, открывают любую страницу таблицы случайных чисел и выписывают под-ряд 50 чисел; в выборку попадают те объекты, номера которых совпадают с выписанными случайными числами. Если бы оказалось, что случайное число таблицы превышает число N, то такое случайное число пропускают. При осуществлении бесповторной выборки случайные числа таблицы, уже встречавшиеся ранее, следует также пропустить.
Типическим называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее «типической» части. Например, если детали изготовляют на нескольких станках, то отбор производят не из всей совокупности деталей, произведенных всеми станками, а из продукдии каждого станка в отдельности. Типическим отбором лользуются тогда, когда обследуемый признак заметно колеблется в различных типических частях генеральной совокупности. Например, если продукция изготовляется на нескольких машинах, среди которых есть более и менее изношенные, то здесь типи-ческий отбор целесообразен.
Механическим называют отбор, при котором генеральную совокупность «мехаяически» делят на столько групп, сколько объектов должно войти в выборку, а из каждой |группы отбирают один объект. Например, если нужно отобрать 20% изготовленных станком деталей, то отби-рают каждую пятую деталь; если требуется отобрать 5% деталей, то отбирают каждую двадцатую деталь, и т. д. Следует указать, что иногда механический отбор может не обеспечить репрезентативности выборки. Например, если отбирают каждый двадцатый обтачиваемый валик, причем сразу же лосле отбора производят замену резца, то отобранными окажутся все валики, обточенные затуплен-ными резцами. В таком случае следует устранить совпа-дение ритма отбора с ритмом замены резца, для чего надо отбирать, скажем, каждый десятый валик из двад-цати обточенных.
Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а «сериями», которые подвергаются сплошному обследованию. Например, если изделия изготовляются большой группой станковавтоматов, то подвергают сплошному обследованию продукцию только нескольких станков. Серийным отбором пользуются тогда, когда обследуемый признак колеблется в различных сериях незначитель-но.
Подчеркнем, что на практике часто применяется комбинированный отбор, при котором сочетаются указанные выше способы. Например, нногда разбивают генеральную совокупность на серии одинакового объема, затем простым случайным отбором выбирают несколько серий и, наконец, из каждой серии простым случайным отбором извлекают отдельные объекты.
Исходные данные
В результате выборочного контроля установлено, что распределение 100 рабочих завода по стажу их работы x (в годах) и выработки изделий y одним из рабочих за смену (в штуках) следующие:
Таблица 1 Распределение рабочих по стажу
| x-y | 0-2 | 2-4 | 4-6 | 6-8 | 8-10 | 10-12 |
| 17-19 | 2 | 4 | 1 | 1 | - | - |
| 19-21 | 1 | 6 | 8 | 1 | - | - |
| 21-23 | - | 2 | 7 | 6 | 2 | 1 |
| 23-25 | - | - | 3 | 18 | 16 | 2 |
| 25-27 | - | 2 | 3 | - | 6 | 8 |
На основании этой таблицы:
Задание №1Построить интервальный и дискретный вариационные ряды для x и y.
Статистическим аналогом ряда распределения называется вариационный ряд, то есть таблица, в верхней строке которой указывают варианты, а в нижней – либо частоты, либо относительные частоты.
Интервальный вариационный ряд.
Таблица 2 Интегральный вариационный ряд по y
|
|
17-19 | 19-21 | 21-23 | 23-25 | 25-27 |
|
|
8 | 16 | 18 | 39 | 19 |
Дискретный вариационный ряд.
Таблица 3 Дискретный вариационный ряд по y
|
|
18 | 20 | 22 | 24 | 26 |
|
|
8 | 16 | 18 | 39 | 19 |
Интервальный вариационный ряд.
Таблица 4 – Интегральный вариационный ряд по x
|
|
0-2 | 2-4 | 4-6 | 6-8 | 8-10 | 10-12 |
|
|
3 | 14 | 22 | 26 | 24 | 11 |
Дискретный вариационный ряд.
Таблица 5 Дискретный вариационный ряд по x
|
|
1 | 3 | 5 | 7 | 9 | 11 |
|
|
3 | 14 | 22 | 26 | 24 | 11 |
Построить полигон распределения и гистограмму частот для x и y. Определить среднее значение, дисперсию, среднеквадратичное отклонение, моду, среднюю варианту, размах варьирования, коэффициент вариации.
Построим гистограмму и полигон частот для y от 17 до 27.
![]()
![]()
Относительная частота попадания:
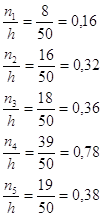
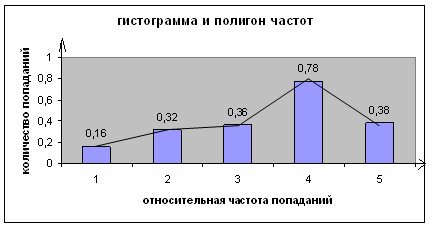
Рисунок 1 Гистограмма и полигон частот для y
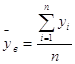
![]()
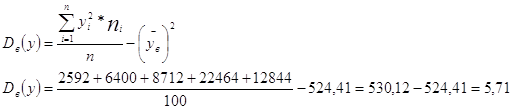
![]()
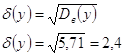
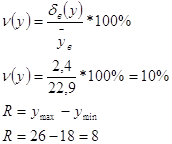
Построим гистограмму и полигон частот для x от 0 до 12.
![]()
![]()
Относительная частота попадания:
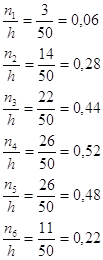
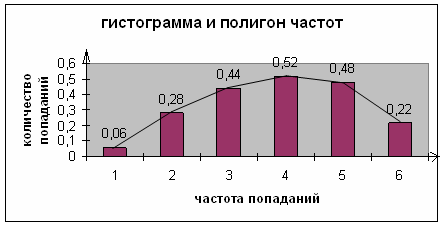
Рисунок 2 Гистограмма и полигон частот для x
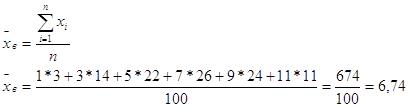
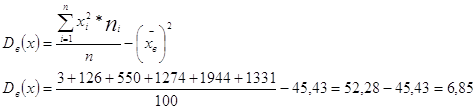
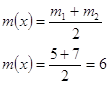
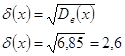
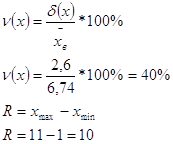
Задание выполняется с помощью макроса, текст которого приведен в приложении А.
Задание №3С надежностью
![]() определить
доверительный интервал для y и необходимый объем выборки для вдвое меньшей
предельной выборки.
определить
доверительный интервал для y и необходимый объем выборки для вдвое меньшей
предельной выборки.
Доверительным
интервалом называется интервал, который с надежностью ![]() покрывает
оцениваемый интервал.
покрывает
оцениваемый интервал.
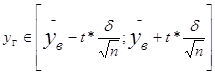 , где
, где
![]() – точность
оценки,
– точность
оценки,
![]() – объем
выборки,
– объем
выборки,
![]() – значение
функции Лапласа
– значение
функции Лапласа
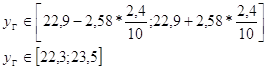
Определяем необходимый объем выборки для вдвое меньшей предельной ошибки.
![]()
![]()
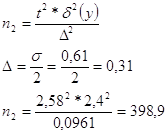
Задание выполняется с помощью макроса, текст приведен в приложение Б.
Задание №4Предполагая распределение количества вырабатываемых за смену изделий одним рабочим – y нормальным, вычислить теоретическую частоту. Проверить значимость расхождения теоретических и эмпирических частот по критерию Пирсона на 1% уровня значимости и сделать вывод о согласовании с опытными данными гипотезы, что количество вырабатываемых изделий за смену (y) распределено по нормальному закону.
Критерием
согласия называется критерий проверки гипотезы о предполагаемом законе
неизвестного распределения. С этой целью будем сравнивать эмпирические
(наблюдаемые) и теоретические значения. Допустим, что в предположенном
нормальном распределении вычислены теоретические частоты (![]() ). При уровне значимости
). При уровне значимости
![]() требуется
проверить нулевую гипотезу (
требуется
проверить нулевую гипотезу (![]() ): генеральная совокупность
распределена нормально. В качестве критерия проверки нулевой гипотезы принимаем
случайную величину
): генеральная совокупность
распределена нормально. В качестве критерия проверки нулевой гипотезы принимаем
случайную величину ![]() .
.
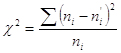
Эта величина случайная, так как в различных опытах она принимает различные заранее неизвестные значения.
Правило: для того чтобы при заданном уровне значимости проверить нулевую гипотезу, надо сначала вычислить теоретические частоты, а затем наблюдаемые значения критерия.
![]()
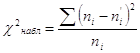
По таблице
критических точек распределения ![]() , по заданному уровню значимости
, по заданному уровню значимости ![]() и числу
степеней свободы
и числу
степеней свободы ![]() , найти критическую точку
, найти критическую точку ![]() . Если
. Если ![]()
![]() – нет оснований
отвергать нулевую гипотезу, если
– нет оснований
отвергать нулевую гипотезу, если
![]() , то нулевая
гипотеза отвергается.
, то нулевая
гипотеза отвергается.
Таблица 6 Данные для проверки расхождения теоретических и эмпирических частот
|
|
|
|
|
|
| 18 | 2,04 | 0,05 | 8 | 4,2 |
| 20 | 1,21 | 0,19 | 16 | 15,8 |
| 22 | 0,4 | 0,37 | 18 | 30,8 |
| 24 | 0,5 | 0,35 | 39 | 29,2 |
| 26 | 1,3 | 0,17 | 19 | 14,2 |
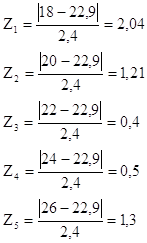
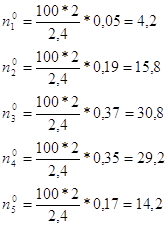
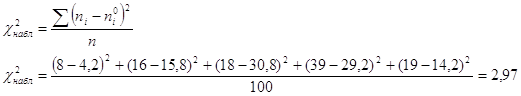
![]()
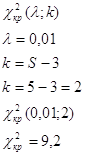
![]() нулевую
гипотезу принимаем.
нулевую
гипотезу принимаем.
Вывод: ![]() распространяется по
нормальному закону.
распространяется по
нормальному закону.
Текст макроса этого задания представлен в приложении В.
Задание №5
Предполагая, что между стажем работы (x) и количеством вырабатываемых за смену изделий (y) существует корреляционная зависимость, определить выборочный коэффициент корреляции и проанализировать степень силы и направление связи.
1
Записываем
![]() и
и ![]() в таблицу.
в таблицу.
Таблица 7 Корреляционная зависимость
|
y |
1 | 3 | 5 | 7 | 9 | 11 |
|
|
||
|
u v |
-3 | -2 | -1 | 0 | 1 | 2 | ||||
| 18 | -2 | 2 | 4 | 1 | 1 | - | - | -15 | 30 | 8 |
| 20 | -1 | 1 | 6 | 8 | 1 | - | - | -23 | 23 | 16 |
| 22 | 0 | - | 2 | 7 | 6 | 2 | 1 | -7 | 0 | 18 |
| 24 | 1 | - | - | 3 | 18 | 16 | 2 | 17 | 17 | 39 |
| 26 | 2 | - | 2 | 3 | - | 6 | 8 | 15 | 30 | 19 |
|
|
-5 | -10 | -1 | 15 | 28 | 18 | ||||
| 15 | 20 | 1 | 0 | 28 | 36 | 100 | ||||
|
|
3 | 14 | 22 | 26 | 24 | 11 |
2 Находим условные варианты.
![]() , где
, где
![]() – «ложные
нули» варианты
– «ложные
нули» варианты ![]() . В качестве «ложного нуля»
берем варианту в середине дискретного ряда.
. В качестве «ложного нуля»
берем варианту в середине дискретного ряда.
![]() – шаг
варианты
– шаг
варианты ![]() .
.
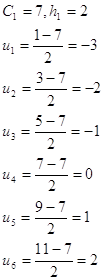
![]() , где
, где
![]() – «ложные
нули» варианты
– «ложные
нули» варианты ![]() ,
,
![]() – шаг
варианты
– шаг
варианты ![]() .
.
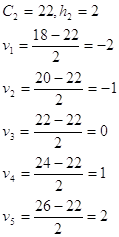
3
Находим
![]()
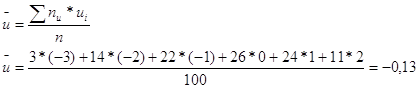
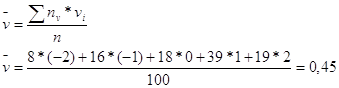
4 Рассчитываем вспомогательные величины.
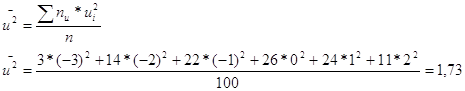
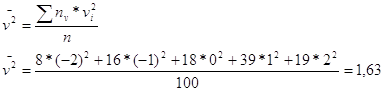
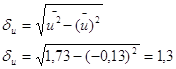
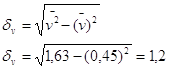
5 Вычисляем коэффициент корреляции.
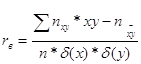 , где
, где
![]() – выборочная
средняя признаков x и y;
– выборочная
средняя признаков x и y;
n – объем выборки;
![]() среднеквадратичное отклонение.
среднеквадратичное отклонение.
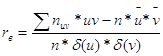
![]() – вычисляется с
помощью таблицы 7.
– вычисляется с
помощью таблицы 7.
![]()
Для оценки
силы линейной корреляционной связи служит выборочный коэффициент корреляции – ![]() . Чем ближе
. Чем ближе ![]() к единице, тем связь
сильнее; чем ближе
к единице, тем связь
сильнее; чем ближе ![]() к нулю, тем связь слабее. Если
к нулю, тем связь слабее. Если ![]() – связь
сильная,
– связь
сильная, ![]() связь средняя,
связь средняя, ![]() – связь слабая.
– связь слабая.
Вывод: так как вычисленный
коэффициент корреляции ![]() =
=![]()
![]() что сила линейной корреляционной
связи сильная.
что сила линейной корреляционной
связи сильная.
Текст макроса представлен в приложении Г.
Задание №6Проверить значимость коэффициента корреляции по критерию Стьюдента.
Проверка
значимости коэффициента корреляции осуществляется по критерию Стьюдента. Данный
коэффициент t сравнивается с табличным ![]() . Если
. Если ![]() , то коэффициент корреляции
значим, и таким образом связь между случайными величинами имеется.
, то коэффициент корреляции
значим, и таким образом связь между случайными величинами имеется.
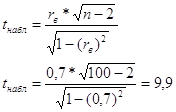
![]()
![]() связь между
случайными величинами имеется – нулевая гипотеза отвергается.
связь между
случайными величинами имеется – нулевая гипотеза отвергается.
Задание выполняется с помощь макроса, текст которого приведен в приложении Д.
Задание №7
Найти уравнение линейной регрессии y(x) и x(y). Построить облако рассеяния, центр распределения и прямые регрессии.
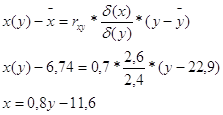
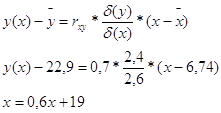
![]()
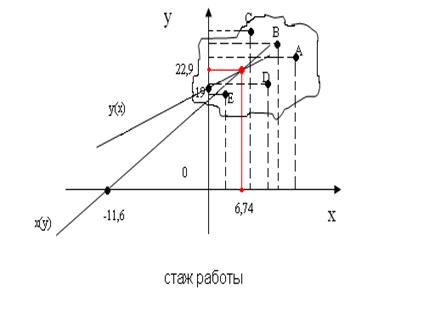
Рисунок 3 – Облако рассеяния
Координаты точек, входящих в облако рассеяния:
А (22,9;24,2); В (19;30,5); С (7,34;40,1); D (16;19,3);
Е (3,75;18,6).
Таблица 8 – Данные для построения прямой х(у)
| х(у) | -11,6 |
| у | 0 |
Таблица 9 – Данные для построения прямой у(х)
| у(х) | 19 |
| х | 0 |
Текст макроса приведен в приложение Е
Задание №8
По соответствующему уравнению регрессии оценить среднее количество вырабатываемых за смену изделий рабочим, имеющим стаж работы 15 лет.
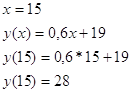
![]()
Среднее количество вырабатываемых за смену изделий рабочим, имеющим стаж работы 15 лет равно 28.
Задание выполняется с помощью макроса, текст которого приведен в приложении Ж.
Задание №9Считая, что возраст работающих подчинен нормальному закону распределения с параметрами (средний возраст – 40 лет, среднеквадратичное отклонение – 7 лет), определить интервал, содержащий практически всевозможные значения их возраста (поле рассеяния) и определить процент работающих мужчин и женщин пенсионного возраста.
Для мужчин:
![]() лет
лет
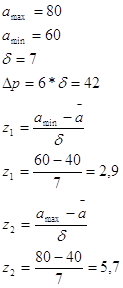
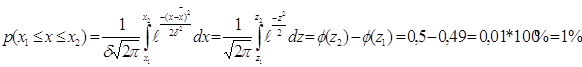
Процент работающих мужчин пенсионного возраста равен 1%
Для женщин:
![]() лет
лет
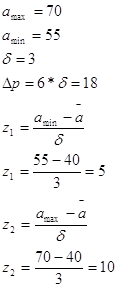
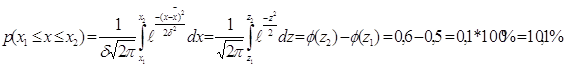
Процент женщин пенсионного возраста работающих на предприятии равен 10,1%.
Текст макроса приведен в приложении З.
Приложение А
(обязательное)
Описание макроса задания №2
Sub Задание2()
Range("C49").Select
ActiveCell.FormulaR1C1 = "=R[-9]C[6]/R[1]C[8]"
Range("C50").Select
ActiveCell.FormulaR1C1 = "=R[-10]C[7]/RC[8]"
Range("C51").Select
ActiveCell.FormulaR1C1 = "=R[-11]C[8]/R[-1]C[8]"
Range("C52").Select
ActiveCell.FormulaR1C1 = "=R[-12]C[9]/R[-2]C[8]"
Range("C53").Select
ActiveCell.FormulaR1C1 = "=R[-13]C[10]/R[-3]C[8]"
Range("C54").Select
ActiveCell.FormulaR1C1 = "=R[-14]C[11]/R[-4]C[8]"
Range("F49").Select
ActiveCell.FormulaR1C1 = "=R[-9]C[-4]/R[1]C[5]"
Range("F50").Select
ActiveCell.FormulaR1C1 = "=R[-10]C[-3]/RC[5]"
Range("F51").Select
ActiveCell.FormulaR1C1 = "=R[-11]C[-2]/R[-1]C[5]"
Range("F52").Select
ActiveCell.FormulaR1C1 = "=R[-12]C[-1]/R[-2]C[5]"
Range("F53").Select
ActiveCell.FormulaR1C1 = "=R[-13]C/R[-3]C[5]"
Range("K52").Select
ActiveCell.FormulaR1C1 = _
"=(R[-12]C[-2]*R[-13]C[-2]+R[-12]C[-1]*R[-13]C[-1]+R[-12]C*R[-13]C+R[-12]C[1]*R[-13]C[1]+R[-12]C[2]*R[-13]C[2]+R[-12]C[3]*R[-13]C[3])/R[-3]C"
Range("K53").Select
ActiveCell.FormulaR1C1 = _
"=(R[-13]C[-9]*R[-14]C[-9]+R[-13]C[-8]*R[-14]C[-8]+R[-13]C[-7]*R[-14]C[-7]+R[-13]C[-6]*R[-14]C[-6]+R[-13]C[-5]*R[-14]C[-5])/R[-4]C"
Range("K54").Select
ActiveCell.FormulaR1C1 = _
"=(R[-14]C[-2]*R[-15]C[-2]^2+R[-14]C[-1]*R[-15]C[-1]^2+R[-14]C*R[-15]C^2+R[-14]C[1]*R[-15]C[1]^2+R[-14]C[2]*R[-15]C[2]^2+R[-14]C[3]*R[-15]C[3]^2)/R[-5]C"
Range("K54").Select
ActiveCell.FormulaR1C1 = _
"=(R[-14]C[-2]*R[-15]C[-2]^2+R[-14]C[-1]*R[-15]C[-1]^2+R[-14]C*R[-15]C^2+R[-14]C[1]*R[-15]C[1]^2+R[-14]C[2]*R[-15]C[2]^2+R[-14]C[3]*R[-15]C[3]^2)/R[-5]C-R[-2]C^2"
Range("K55").Select
ActiveCell.FormulaR1C1 = _
"=(R[-15]C[-9]*R[-16]C[-9]^2+R[-15]C[-8]*R[-16]C[-8]^2+R[-15]C[-7]*R[-16]C[-7]^2+R[-15]C[-6]*R[-16]C[-6]^2+R[-15]C[-5]*R[-16]C[-5]^2)/R[-6]C-R[-2]C^2"
Range("K55").Select
ActiveCell.FormulaR1C1 = _
"=(R[-15]C[-9]*R[-16]C[-9]^2+R[-15]C[-8]*R[-16]C[-8]^2+R[-15]C[-7]*R[-16]C[-7]^2+R[-15]C[-6]*R[-16]C[-6]^2+R[-15]C[-5]*R[-16]C[-5]^2)/R[-6]C-R[-2]C^2"
Range("K55").Select
ActiveCell.FormulaR1C1 = _
"=(R[-15]C[-9]*R[-16]C[-9]^2+R[-15]C[-8]*R[-16]C[-8]^2+R[-15]C[-7]*R[-16]C[-7]^2+R[-15]C[-6]*R[-16]C[-6]^2+R[-15]C[-5]*R[-16]C[-5]^2)/R[-6]C-R[-2]C^2"
Range("K56").Select
ActiveCell.FormulaR1C1 = "=SQRT(R[-2]C)"
Range("K57").Select
ActiveCell.FormulaR1C1 = "=SQRT(R[-2]C)"
Range("K58").Select
ActiveWindow.SmallScroll Down:=6
ActiveCell.FormulaR1C1 = "=(R[-19]C+R[-19]C[1])/2"
Range("K59").Select
ActiveCell.FormulaR1C1 = "=R[-20]C[-7]"
Range("K60").Select
ActiveWindow.SmallScroll Down:=6
ActiveCell.FormulaR1C1 = "=R[-21]C[3]-R[-21]C[-2]"
Range("K61").Select
ActiveWindow.SmallScroll Down:=9
ActiveCell.FormulaR1C1 = "=R[-22]C[-5]-R[-22]C[-9]"
Range("K62").Select
ActiveWindow.SmallScroll Down:=9
ActiveCell.FormulaR1C1 = "=R[-6]C/R[-10]C*100"
Range("K63").Select
ActiveCell.FormulaR1C1 = "=R[-6]C/R[-10]C*100"
Range("K63").Select
ActiveCell.FormulaR1C1 = "=R[-6]C/R[-10]C*100"
Range("K64").Select
End Sub
Приложение Б
(обязательное)
Описание макроса задание №3
Sub Задание3()
' Range("G80").Select
ActiveCell.FormulaR1C1 = "=(R[1]C[-4]*R[-23]C[4])/(SQRT(R[-31]C[4]))"
Range("G81").Select
ActiveWindow.SmallScroll Down:=6
ActiveCell.FormulaR1C1 = "=R[-1]C/2"
Range("G83").Select
ActiveCell.FormulaR1C1 = "=R[-30]C[4]-R[-3]C"
Range("H83").Select
ActiveCell.FormulaR1C1 = "=R[-30]C[3]+R[-2]C[-1]"
Range("D85").Select
ActiveCell.FormulaR1C1 = "=R[-4]C[-1]^2*R[-28]C[7]^2/R[-4]C[3]^2"
Range("D86").Select
End Sub
Приложение В
(обязательное)
Описание макроса задание №4
Sub Задание4()
Range("B96").Select
ActiveCell.FormulaR1C1 = "=R[-57]C"
Range("B97").Select
ActiveCell.FormulaR1C1 = "=R[-58]C[1]"
Range("B98").Select
ActiveCell.FormulaR1C1 = "=R[-59]C[2]"
Range("B99").Select
ActiveCell.FormulaR1C1 = "=R[-60]C[3]"
Range("B100").Select
ActiveCell.FormulaR1C1 = "=R[-61]C[4]"
Range("E96").Select
ActiveCell.FormulaR1C1 = "=R[-56]C[-3]"
Range("E97").Select
ActiveCell.FormulaR1C1 = "=R[-57]C[-2]"
Range("E98").Select
ActiveCell.FormulaR1C1 = "=R[-58]C[-1]"
Range("E99").Select
ActiveCell.FormulaR1C1 = "=R[-59]C"
Range("E100").Select
ActiveCell.FormulaR1C1 = "=R[-60]C[1]"
Range("C96").Select
ActiveCell.FormulaR1C1 = "=(RC[-1]-R53C11)/R57C11"
Range("C97").Select
ActiveWindow.SmallScroll Down:=9
Range("C96").Select
Selection.AutoFill Destination:=Range("C96:C100"), Type:=xlFillDefault
Range("C96:C100").Select
Range("F96").Select
ActiveCell.FormulaR1C1 = "=(R49C11*R102C7/R57C11)*RC[-2]"
Range("F96").Select
Selection.AutoFill Destination:=Range("F96:F100"), Type:=xlFillDefault
Range("F96:F100").Select
ActiveWindow.SmallScroll Down:=3
Range("G102").Select
ActiveCell.FormulaR1C1 = "=RC[-3]-3"
Range("G99:P99").Select
ActiveCell.FormulaR1C1 = _
"=IF(R[4]C[-4]<R[4]C,""Нулевая гипотеза принимается (Y распределен по нормальному закону)"",""Нулевая гипотеза отвергается (Y не распределен по нормальному закону)"")"
Range("C103").Select
ActiveCell.FormulaR1C1 = _
"=(R[-7]C[2]-R[-7]C[3])^2/R[-7]C[3]+(R[-6]C[2]-R[-6]C[3])^2/R[-6]C[3]+(R[-5]C[2]-R[-5]C[3])^2/R[-5]C[3]+(R[-4]C[2]-R[-4]C[3])^2/R[-4]C[3]+(R[-3]C[2]-R[-3]C[3])^2/R[-3]C[3]"
Range("C104").Select
ActiveWindow.SmallScroll Down:=-6
End Sub
Приложение Г
(обязательное)
Описание макроса задание №5
Sub Задание5()
Задание5 Макрос
Range("C105").Select
ActiveCell.FormulaR1C1 = "=R[-68]C[-1]"
Range("C106").Select
ActiveWindow.SmallScroll Down:=6
Range("C105").Select
Selection.AutoFill Destination:=Range("C105:H105"), Type:=xlFillDefault
Range("C105:H105").Select
ActiveWindow.SmallScroll Down:=6
Range("C114").Select
ActiveCell.FormulaR1C1 = "=R[-76]C[-1]"
Range("C114").Select
Selection.AutoFill Destination:=Range("C114:H114"), Type:=xlFillDefault
Range("C114:H114").Select
Range("A107").Select
ActiveCell.FormulaR1C1 = "=R[-70]C[9]"
Range("A108").Select
ActiveCell.FormulaR1C1 = "=R[-71]C[10]"
Range("A109").Select
ActiveCell.FormulaR1C1 = "=R[-72]C[11]"
Range("A110").Select
ActiveCell.FormulaR1C1 = "=R[-73]C[12]"
Range("A111").Select
ActiveCell.FormulaR1C1 = "=R[-74]C[13]"
Range("K107").Select
ActiveCell.FormulaR1C1 = "="
Range("K107").Select
ActiveCell.FormulaR1C1 = "=R[-69]C[-1]"
Range("K108").Select
ActiveCell.FormulaR1C1 = "=R[-70]C"
Range("K109").Select
ActiveCell.FormulaR1C1 = "=R[-71]C[1]"
Range("K110").Select
ActiveCell.FormulaR1C1 = "=R[-72]C[2]"
Range("K111").Select
ActiveCell.FormulaR1C1 = "=R[-73]C[3]"
Range("K112").Select
ActiveWindow.SmallScroll Down:=9
Range("C107").Select
ActiveCell.FormulaR1C1 = "=R[-91]C[2]"
Range("C108").Select
ActiveWindow.SmallScroll Down:=9
Range("C107").Select
Selection.AutoFill Destination:=Range("C107:H107"), Type:=xlFillDefault
Range("C107:H107").Select
Range("C108").Select
ActiveCell.FormulaR1C1 = "=R[-91]C[2]"
Range("C108").Select
Selection.AutoFill Destination:=Range("C108:H108"), Type:=xlFillDefault
Range("C108:H108").Select
Range("C109").Select
ActiveCell.FormulaR1C1 = "=R[-91]C[2]"
Range("C110").Select
ActiveWindow.SmallScroll Down:=6
Range("C109").Select
Selection.AutoFill Destination:=Range("C109:H109"), Type:=xlFillDefault
Range("C109:H109").Select
Range("C110").Select
ActiveCell.FormulaR1C1 = "=R[-91]C[2]"
Range("C111").Select
ActiveWindow.SmallScroll Down:=9
Range("C110").Select
Selection.AutoFill Destination:=Range("C110:H110"), Type:=xlFillDefault
Range("C110:H110").Select
Range("C111").Select
ActiveCell.FormulaR1C1 = "=R[-91]C[2]"
Range("C112").Select
ActiveWindow.SmallScroll Down:=6
Range("C111").Select
Selection.AutoFill Destination:=Range("C111:H111"), Type:=xlFillDefault
Range("C111:H111").Select
Range("C106").Select
ActiveCell.FormulaR1C1 = "=(R[-1]C-R118C11)/R116C11"
Range("C106").Select
Selection.AutoFill Destination:=Range("C106:H106"), Type:=xlFillDefault
Range("C106:H106").Select
Range("B107").Select
ActiveCell.FormulaR1C1 = "=(RC[-1]-R119C11)/R117C11"
Range("B107").Select
Selection.AutoFill Destination:=Range("B107:B111"), Type:=xlFillDefault
Range("B107:B111").Select
Range("I107").Select
ActiveCell.FormulaR1C1 = _
"=R[-1]C[-6]*RC[-6]+R[-1]C[-5]*RC[-5]+R[-1]C[-4]*RC[-4]+R[-1]C[-3]*RC[-3]+R[-1]C[-2]*RC[-2]+R[-1]C[-1]*R[-1]C[-1]"
Range("I107").Select
ActiveCell.FormulaR1C1 = _
"=R[-1]C[-6]*RC[-6]+R[-1]C[-5]*RC[-5]+R[-1]C[-4]*RC[-4]+R[-1]C[-3]*RC[-3]+R[-1]C[-2]*RC[-2]+R[-1]C[-1]*RC[-1]"
Range("I107").Select
ActiveCell.FormulaR1C1 = _
"=R106C3*RC[-6]+R106C4*RC[-5]+R106C5*RC[-4]+R106C6*RC[-3]+R106C7*RC[-2]+R106C8*RC[-1]"
Range("I107").Select
Selection.AutoFill Destination:=Range("I107:I111"), Type:=xlFillDefault
Range("I107:I111").Select
Range("B107").Select
ActiveCell.FormulaR1C1 = ""
Range("C112").Select
ActiveCell.FormulaR1C1 = ""
Range("B108").Select
Selection.Copy
Range("B107").Select
ActiveSheet.Paste
Range("B109").Select
Application.CutCopyMode = False
ActiveCell.FormulaR1C1 = "=(RC[-1]-R119C11)/R117C11"
Range("C112").Select
ActiveCell.FormulaR1C1 = _
"=R107C2*R[-5]C+R108C2*R[-4]C+R109C2*R[-3]C+R110C2*R[-2]C+R111C2*R[-1]C"
Range("C113").Select
ActiveWindow.SmallScroll Down:=-6
Range("C112").Select
Selection.AutoFill Destination:=Range("C112:H112"), Type:=xlFillDefault
Range("C112:H112").Select
Range("C113").Select
ActiveCell.FormulaR1C1 = "=R[-1]C*R[-7]C"
Range("C113").Select
Selection.AutoFill Destination:=Range("C113:H113"), Type:=xlFillDefault
Range("C113:H113").Select
Range("J107").Select
ActiveCell.FormulaR1C1 = "=RC[-1]*RC[-8]"
Range("J107").Select
Selection.AutoFill Destination:=Range("J107:J111"), Type:=xlFillDefault
Range("J107:J111").Select
Range("J112").Select
Selection.FormulaR1C1 = "="
ActiveCell.FormulaR1C1 = "=SUM(R[-5]C:R[-1]C)"
Range("J113").Select
Selection.FormulaR1C1 = "="
ActiveCell.FormulaR1C1 = "=SUM(RC[-7]:RC[-2])"
Range("C116").Select
ActiveCell.FormulaR1C1 = _
"=(R[-2]C*R[-10]C+R[-2]C[1]*R[-10]C[1]+R[-2]C[2]*R[-10]C[2]+R[-2]C[3]*R[-10]C[3]+R[-2]C[4]*R[-10]C[4]+R[-2]C[5]*R[-10]C[5])/R[-67]C[1]"
Range("C117").Select
ActiveWindow.SmallScroll Down:=9
Range("C117").Select
ActiveCell.FormulaR1C1 = _
"=(R[-10]C[8]*R[-10]C[-1]+R[-9]C[8]*R[-9]C[-1]+R[-8]C[8]*R[-8]C[-1]+R[-7]C[8]*R[-7]C[-1]+R[-6]C[8]*R[-6]C[-1])/R[-68]C[1]"
Range("C118").Select
ActiveWindow.SmallScroll Down:=6
ActiveCell.FormulaR1C1 = _
"=(R[-4]C*R106C3+R[-4]C[1]*R106C4+R[-4]C[2]*R106C5+R[-4]C[3]*R106C6+R[-4]C[4]*R106C7+R[-4]C[5]*R106C8)/R[-69]C[1]"
Range("C119").Select
ActiveWindow.SmallScroll Down:=6
Range("C118").Select
ActiveCell.FormulaR1C1 = _
"=(R[-4]C*R106C3^2+R[-4]C[1]*R106C4^2+R[-4]C[2]*R106C5^2+R[-4]C[3]*R106C6^2+R[-4]C[4]*R106C7^2+R[-4]C[5]*R106C8^2)/R[-69]C[1]"
Range("C119").Select
ActiveCell.FormulaR1C1 = _
"=(R[-12]C[8]*R[-12]C[-1]^2+R[-11]C[8]*R[-11]C[-1]^2+R[-10]C[8]*R[-10]C[-1]^2+R[-9]C[8]*R[-9]C[-1]^2+R[-8]C[8]*R[-8]C[-1]^2)/R[-70]C[1]"
Range("F116").Select
ActiveCell.FormulaR1C1 = "=SQRT(R[2]C[-3]-RC[-3]^2)"
Range("F117").Select
ActiveCell.FormulaR1C1 = "=коень(R[2]C[-3]-RC[-3]^2)"
Range("F117").Select
Columns("F:F").ColumnWidth = 11
Columns("F:F").ColumnWidth = 10.14
ActiveCell.FormulaR1C1 = "=SQRT(R[2]C[-3]-RC[-3]^2)"
Range("F118").Select
ActiveCell.FormulaR1C1 = "=R[-5]C[4]"
Range("F119").Select
ActiveCell.FormulaR1C1 = _
"=(R[-1]C-R[-70]C[-2]*R[-3]C[-3]*R[-2]C[-3])/(R[-70]C[-2]*R[-3]C*R[-2]C)"
Range("F120").Select
ActiveCell.FormulaR1C1 = _
"=IF(AND(R[-1]C>0.7,R[-1]C<1),""связь сильная"",IF(AND(R[-1]C>0.5,R[-1]C<0.7),""связь средняя"",""связь слабая""))"
Range("F121").Select
End Sub
Приложение Д
(обязательное)
Описание макроса задание №6
Sub Задание6()
Range("J126").Select
ActiveCell.FormulaR1C1 = "=R[-7]C[-4]*корень"
Range("D49").Select
ActiveWindow.SmallScroll Down:=75
Range("J126").Select
ActiveCell.FormulaR1C1 = _
"=(R[-7]C[-4]*SQRT(R[-77]C[-6]-2))/коернь(1-R[-7]C[-4]^2)"
Range("J126").Select
Columns("J:J").ColumnWidth = 11.86
Columns("J:J").ColumnWidth = 13.86
Columns("J:J").ColumnWidth = 9.86
Columns("J:J").ColumnWidth = 8.43
ActiveCell.FormulaR1C1 = _
"=(R[-7]C[-4]*SQRT(R[-77]C[-6]-2))/коернь(1-(R[-7]C[-4]^2))"
Range("J126").Select
ActiveCell.FormulaR1C1 = _
"=(R[-7]C[-4]*SQRT(R[-77]C[-6]-2))/SQRT(1-(R[-7]C[-4]^2))"
Range("H124").Select
ActiveCell.FormulaR1C1 = _
"=IF(R[2]C[2]>R[2]C[-1],""Связи между случайными величинами нет (нулевая гипотеза отвергается)"",""Связь между случайными величинами есть (нулевая гипотеза подтверждается)"")"
Range("H125").Select
End Sub
Приложение Е
(обязательное)
Описание макроса задание №7
Sub Задание7()
Range("B141").Select
ActiveCell.FormulaR1C1 = _
"=R[-13]C[6]*(R[-85]C[9]/R[-84]C[9])*(R[1]C-R[-88]C[9])+R[-89]C[9]"
Range("D141").Select
ActiveCell.FormulaR1C1 = _
"=R128C8*(R57C11/R56C11)*(R[1]C-R52C11)+R53C11"
Range("C144").Select
ActiveCell.FormulaR1C1 = "=R128C8*(R57C11/R56C11)*(R[1]C-R52C11)+R53C11"
Range("C144").Select
Selection.AutoFill Destination:=Range("C144:D144"), Type:=xlFillDefault
Range("C144:D144").Select
Range("C147").Select
ActiveCell.FormulaR1C1 = "=R128C8*(R56C11/R57C11)*(R[1]C-R53C11)+R52C11"
Range("C147").Select
Selection.AutoFill Destination:=Range("C147:D147"), Type:=xlFillDefault
Range("C147:D147").Select
Range("C144").Select
End Sub
Приложение Ж
(обязательное)
Описание макроса задание №8
Sub Задание8()
Range("D157").Select
ActiveCell.FormulaR1C1 = _
"=R[-29]C[4]*(R[-100]C[7]/R[-101]C[7])*(R[1]C-R[-105]C[7])-R[-104]C[7]"
Range("D157").Select
ActiveCell.FormulaR1C1 = _
"=R[-29]C[4]*(R[-100]C[7]/R[-101]C[7])*(R[1]C-R[-105]C[7])+R[-104]C[7]"
Range("D158").Select
End Sub
Приложение З
(обязательное)
Описание макроса задание №9
Sub Задание9()
ActiveWindow.SmallScroll Down:=6
Range("C170").Select
ActiveCell.FormulaR1C1 = "=(R[-3]C[3]-R[-3]C)/R[-2]C"
Range("C171").Select
ActiveCell.FormulaR1C1 = "=(R[-3]C[3]-R[-4]C)/R[-3]C"
Range("C172").Select
ActiveWindow.SmallScroll Down:=3
Range("C178").Select
ActiveCell.FormulaR1C1 = "=(R[-3]C[3]-R[-3]C)/R[-2]C"
Range("C179").Select
ActiveCell.FormulaR1C1 = "=(R[-3]C[3]-R[-4]C)/R[-3]C"
Range("L170").Select
ActiveCell.FormulaR1C1 = "=(R[-2]C[-3]-R[-2]C[-1])*100"
Range("L178").Select
ActiveCell.FormulaR1C1 = "=(R[-2]C[-3]-R[-2]C[-1])*100"
Range("L179").Select
Range("E170").Select
ActiveCell.FormulaR1C1 = "=R[-2]C[-2]*6"
Range("E178").Select
ActiveCell.FormulaR1C1 = "=R[-2]C[-2]*6"
Range("E179").Select
End Sub
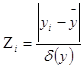
 x
x