Научные и курсовые работы |
Главная
Исторические личности
Военная кафедра
Ботаника и сельское хозяйство
Бухгалтерский учет и аудит
Валютные отношения
Ветеринария
География
Геодезия
Геология
Геополитика
Государство и право
Гражданское право и процесс
Естествознанию
Журналистика
Зарубежная литература
Зоология
Инвестиции
Информатика
История техники
Кибернетика
Коммуникация и связь
Косметология
Кредитование
Криминалистика
Криминология
Кулинария
Культурология
Логика
Логистика
Маркетинг
Наука и техника Карта сайта
Учебное пособие: Технология цифровой связи
Учебное пособие: Технология цифровой связи
НЕКОММЕРЧЕСКОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО
АЛМАТИНСКИИ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра автоматической электросвязи
ТЕХНОЛОГИИ ЦИФРОВОЙ СВЯЗИ
Конспект лекций
для студентов всех форм обучения специальности 050719 – Радиотехника, электроника и телекоммуникации
Алматы 2008
СОСТАВИТЕЛИ: К.С.Чежимбаева, Д.А.Абиров. Технологии цифровой связи. Конспект лекций для студентов всех форм обучения специальности 050719 – Радиотехника, электроника и телекоммуникации.- Алматы: АИЭС, 2008.- 61с.
Конспект лекций посвящен вопросам элементов систем цифровой связи, каналам связи и их характеристикам, узкополосной передаче, методам цифровой модуляции, методам синхронизации, методам и устройствам помехоустойчивого кодирования, принципам применение системы связи с обратной связью и применению эффективного кодирования для сжатия данных, которые необходимы при изучении дисциплин, связанных с этой тематикой. Конспект лекций предназначен для студентов всех форм обучения по специальности 050719 – Радиотехника, электроника и телекоммуникации.
Содержание
Введение
1 Лекция №1. Элементы систем цифровой связи
1.1 Функциональная схема и основные элементы цифровой системы
2 Лекция №2. Каналы связи и их характеристики
2.1 Понятие каналов связи
2.2 Проводные каналы
2.3 Волоконно-оптические каналы
2.4 Беспроводные (радио) каналы
3 Лекция №3. Математические модели каналов связи
3.1 Математические модели каналов связи
4 Лекция №4. Узкополосная передача
4.1 Демодуляция и обнаружения
4.2 Обнаружение сигнала в гауссовом шуме
4.3 Согласованный фильтр
4.4. Межсимвольная интерференция
5 Лекция №5. Алгоритмы цифрового кодирования
5.1 Алгоритмы цифрового кодирования
5.2 Биполярный метод
5.3 Псевдотроичный метод
5.4 Парно – селективный троичный код
6 Лекция №6. Полосовая модуляция и демодуляция
6.1 Методы цифровой полосовой модуляции
6.2 Многопозиционная модуляция
6.3 Амплитудная манипуляция
7 Лекция №7 Оптимальный прием ДС сигнала
7.1 Оптимальный прием ДС сигнала
8 Лекция №8 Спектральные характеристики модулированных колебаний
8.1 Спектральные характеристики модулированных колебаний
8.2 Оптимальный приемник
8.3 Когерентный и некогерентный прием
8.4 Цифровой согласованный фильтр
8.5 Оценка помехоустойчивости модулированных сигналов
9 Лекция №9. Методы синхронизации в ЦСС
9.1 Синхронизация в синхронных и асинхронных системах
9.2 Синхронизация поэлементная, групповая и цикловая
10 Лекция №10 Методы и устройства помехоустойчивого кодирования
10.1 Основные принципы обнаружения и исправления ошибок
10.2 Кодовые расстояние и корректирующая способность кода
10.3 Классификация корректирующих кодов
11 Лекция №11.Помехоустойчивые коды и методы декодирования корректирующих кодов
11.1 Коды Рида – Соломона
12 Лекция №12. Системы связи с обратной связью
12.1 Характеристики систем с обратной связью и их особенности
12.2 Структурная схема системы с информационной обратной связью (ИОС) и решающей обратной связью (РОС), характеристики и алгоритмы работы
13 Лекция №13. Сжатие данных в ЦСС
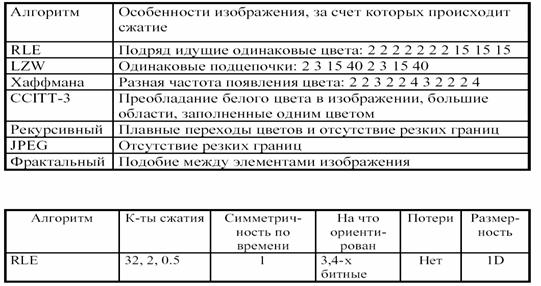
13.1 Алгоритмы сжатия без потерь
Заключение
Список литературы
Введение
В этих конспектах лекции мы представляем основные принципы, которые лежат в основе анализа и синтеза систем цифровой связи. Предмет цифровой связи включает в себя передачу информации в цифровой форме от источника, который создаёт информацию для одного или многих мест назначения. Особенно важным для анализа и синтеза систем связи являются характеристики физических каналов, через которые передаётся информация. Характеристики канала обычно влияют на синтез базовых составных блоков системы связи. Ниже мы опишем элементы системы связи и их функции.
Развитие телекоммуникационных сетей увеличивает роль и значение передачи дискретных сообщений в электросвязи.
Целью дисциплины является изложение принципов и методов передачи цифровых сигналов, научных основ и современное состояние технологии цифровой связи; дать представление о возможностях и естественных границах реализации цифровых систем передачи и обработки, уяснить закономерности, определяющие свойства устройств передачи данных и задачи их функционирования.
Следует отметить, что самая ранняя форма электрической связи, а именно телеграфная связь, была системой цифровой связи. Электрический телеграф был разработан Сэмюэлём Морзе и демонстрировался в 1837 г. Морзе изобрел двоичный код переменой длины, в котором буквы английского алфавита представлены последовательностью точек и тире (кодовые слова). В этом коде часто встречающиеся буквы представлены короткими кодовыми словами, в то время как буквы, встречающиеся менее часто, — более короткими кодовыми словами. Таким образом, код Морзе был предшественником методов кодирования источников кодом переменной длины.
Почти 40 годами позже, в 1875г., Эмиль Бодо изобрёл код для телеграфной связи, в котором каждая буква кодировалась двоичным кодом фиксированной длины 5. В коде Бодо элементы двоичного кода имеют равную длину и именуются посылкой и паузой.
Хотя Морзе принадлежит первая электрическая система цифровой связи (телеграфная связь), начало того, что мы теперь считаем современной теорией цифровой связи, следует из работ Найквиста (1924), исследовавшего проблему определения максимальной скорости передачи, которую можно обеспечить по телеграфному каналу данной ширины полосы частот без межсимвольной интерференции (МСИ). Он сформулировал модель телеграфной системы, в которой передаваемый сигнал имеет общую форму
![]() (1.1)
(1.1)
где g(t) - базовая форма импульса (несущей); {аn} - последовательность данных в двоичном коде (±1), передаваемых со скоростью 1/Гбит/с.
Найквист пытался определить оптимальную форму импульса g(t) с ограниченной полосой W Гц и максимизировать скорость передачи данных в предположении, что импульс не вызывает МСИ в точках отсчёта kT, k = 0,± 1,±2,... Эти исследования привели его к заключению, что максимальная скорость передачи равна 2W отсч./с. Эту скорость теперь называют скоростью Найквиста. Более того, эту скорость передачи можно достичь при использовании импульса g(t) = sin2πWt/(2πWt). Эта форма импульса допускает восстановление данных без межсимвольных помех в выборочные моменты времени. Результат Найквиста эквивалентен версии теоремы отсчётов для сигналов с Ограниченной полосой, который был позже точно сформулирован Шенноном (1948). Теорема отсчётов гласит, что сигнал с шириной полосы частот W может быть восстановлен по его отсчётам, взятым со скоростью Найквиста 2W, путем использования интерполяционной формулы
![]() (1.2)
(1.2)
В продолжение работы Найквиста Хартли (1928) рассмотрел вопрос о
количестве данных, которые могут быть переданы надежно по каналу с ограниченной
полосой частот, когда для последовательной передачи данных используются
импульсы со многими амплитудными уровнями. С учетом шума и другой интерференции
Хартли показал, что приемник может надежно оценивать амплитуду принятого
сигнала с некоторой точностью ![]() . Это исследование привело
Хартли к заключению, что имеется максимальная скорость передачи данных по
каналу с ограниченной полосой частот, зависящая от максимальной амплитуды
сигнала Аmах (фиксированной максимальной
мощности) и величины
. Это исследование привело
Хартли к заключению, что имеется максимальная скорость передачи данных по
каналу с ограниченной полосой частот, зависящая от максимальной амплитуды
сигнала Аmах (фиксированной максимальной
мощности) и величины ![]() .
.
Другим значительным вкладом в развитие теории связи была работа Винера (1942), который рассмотрел проблему оценивания полезного сигнала s(f) на фоне аддитивного шума n(f), исходя из наблюдения принимаемого сигнала r(t) = s(t) + n(t) . Эта проблема возникает при демодуляции сигналов. Винер определил линейный фильтр, выход которого является лучшей среднеквадратической аппроксимацией полезного сигнала s(f). Полученный фильтр назван оптимальным линейным (винеровским) фильтром.
Результаты Хартли и Найквиста по максимальной скорости передачи цифровой информации были предшественниками работ Шеннона (1948), который установил математические основы передачи информации по каналам связи и нашел фундаментальные ограничения для систем цифровой связи. В своей пионерской работе Шеннон сформулировал основную проблему надежной передачи информации в терминах статистической теории связи, используя вероятностные модели для информационных источников и каналов связи. Применяя вероятностный подход, он нашёл универсальную логарифмическую меру для количества информации источника. Он также показал, что существует некоторый предельный показатель, характеризующий скорость передачи информации по каналу связи, зависящий от величины мощности передатчика, ширины полосы и интенсивности аддитивного шума, названный им пропускной способностью канала. Например, в случае аддитивного белого (с равномерным спектром) гауссовского шума идеальный частотно-ограниченный канал с шириной полосы W имеет пропускную способность С', бит/с, которая определяется формулой
![]()
где Р - средняя мощность сигнала, a nq - спектральная плотность мощности аддитивного шума. Значение параметра пропускной способности канала С' состоит в том, что если информационная скорость (производительность) источника R меньше, чем C'(R < С') , то теоретически возможно обеспечить надёжную (свободную от ошибок) передачу через канал соответствующим кодированием. С другой стороны, если R > С' , то надежная передача невозможна, независимо от способов обработки сигнала на передаче и приеме. Таким образом, Шеннон установил основные ограничения передачи информации и породил новое направление, которое теперь называется теорией информации.
Другой важный вклад в области цифровой связи - это работа Котельникова (1947), который провел тщательный анализ различных систем цифровой связи, основанный на геометрическом представлении.
Исследование Котельникова было позже развито Возенкрафтом и Джекобсом (1965).
Вслед публикациям Шеннона появилась классическая работа Хемминга (1950) по кодам с обнаружением и с исправлением ошибок, которые противодействуют вредному влиянию канального шума. Работа Хемминга стимулировала многих исследователей, которые в последующие годы открыли ряд новых и мощных кодов, многие из которых сегодня внедрены в современные системы связи.
За ранними работами Шеннона, Котельникова и Хемминга появилось много новых достижений в области цифровой связи. Некоторые из наиболее заметных достижений следующие:
разработка новых блоковых кодов Маллером (1954), Ридом (1954) и Соломоном (1960), Боузом и Рой-Чоудхури (1960) и Гоппом (1970)
Данные о дисциплине: Название «Технологии цифровой связи».
По данной дисциплине проводятся лекционные и практические занятия, проводятся лабораторные работы, кроме того, предполагается выполнение курсовая работа, собирается схема с применением пакета «System View» для моделирования телекоммуникационных систем, кодирующего и декодирующего устройства циклического кода с использованием модуляции и демодуляции и проведение самостоятельных работ с целью углубления общих знаний теории.
Кредиты |
Курс |
Семестр |
Лекции |
Практическиезанятия |
Лаборат.работы |
Курсовой проект |
Экзамен |
3 |
3 |
6 |
1.5 (26час.) |
1 (17 час.) |
0.5 (17 час.) |
6 |
6 |
1 Лекция №1. Элементы систем цифровой связи
Цель лекции: изучение основных элементов систем цифровой связи и классификации сигналов.
Содержание:
а) функциональная схема и основные элементы цифровой системы;
б) цифровые сигналы.
1.1 Функциональная схема и основные элементы цифровой системы
Функциональную схему и основные элементы цифровой системы связи поясняет рисунке 1.1. Выход источника может быть либо аналоговым сигналом, как звуковой или видеосигнал, либо цифровым сигналом, как выход печатающей машины, - он дискретен во времени и имеет конечное число выходных значений. В системе цифровой связи сообщения, выданные источником, преобразуются в последовательность двоичных символов. В идеале мы можем представить выход источника сообщения небольшим числом двоичных символов (насколько это возможно). Другими словами, мы ищем эффективное представление выхода источника, которое приводит к источнику с наименьшей избыточностью или с полным её отсутствием. Процесс эффективного преобразования выхода источника - как аналогового, так и цифрового - в последовательность двоичных символов называют кодированием источника или сжатием данных.
Последовательность двоичных символов от кодера источника, который мы назовём источником информации, поступает на кодер канала. Цель кодера канала состоит в том, чтобы ввести управляемым способом некоторую избыточность в информационную двоичную последовательность, которая может использоваться в приёмнике, чтобы преодолеть влияние шума и интерференции, с которой сталкиваются, при передачи сигнала через канал. Таким образом, добавленная избыточность служит для увеличения надёжности принятых данных и улучшает верность воспроизведения принятого сигнала. Фактически избыточность в информационной последовательности помогает приёмнику в декодировании переданной информационной последовательности. Например, тривиальной формой кодирования исходной двоичной последовательности является простое повторение каждого двоичного символа т раз, где т - некоторое целое положительное число. Более сложное (нетривиальное) кодирование сводится к преобразованию блока из k информационных символ в уникальную последовательность из n символов, называемую кодовым словом. Значение избыточности, вводимой при кодировании данных таким способом, измеряется отношением n/k. Обратная величина этого отношения, а именно: k/n, названа скоростью кода.
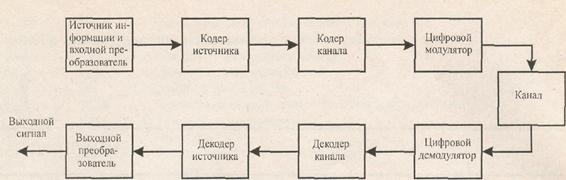
Рисунок 1.1 - Основные элементы цифровой системы связи
Двоичная последовательность на выходе кодера канала поступает на цифровой модулятор, который служит интерфейсом к каналу связи. Так как почти все каналы связи, с которыми сталкиваются на практике, способны к передаче электрических сигналов (волновых процессов), основная цель цифрового модулятора сводится к отображению информационной двоичной последовательности в соответствующий сигнал. Чтобы разобраться с этим вопросом, предположим, что кодированная информационная последовательность должна передать один бит за определённое время с постоянной скоростью R бит/с. Цифровой модулятор может просто отображать двоичный символ 0 в сигнал s0(t), а двоичный символ 1 - в сигнал s1(t). Таким способом каждый бит кодера передаётся отдельно. Мы называем это двоичной модуляцией. В качестве альтернативы модулятор может передавать b кодированных информационных битов одновременно, используя различные сигналы si(t), i=0, ..., M-l, один сигнал для каждого из М-1 возможных b-битовых последовательностей. Мы назовём это М- позиционной модуляцией (М>2). Заметим, что информационная последовательность с b битами поступает на вход модулятора каждые b/R секунд. Следовательно, когда канальная скорость передачи данных R фиксирована, для передачи одного из М сигналов, соответствующих информационной последователь-ности из b бит, отведён в b раз больший интервал времени, чем при двоичной модуляции.
Канал связи - это физическая среда, которая используется для передачи сигнала от передатчика к приёмнику. При беспроволочной связи каналом может быть атмосфера (свободное пространство). С другой стороны, телефонные каналы обычно используют ряд физических сред, включая линии проводной связи, волоконно-оптические кабели и беспроволочные линии (например, микроволновую радиолинию). Для любой физической среды, используемой для передачи информации, существенно, что передаваемый сигнал подвержен случайным искажениям через такие механизмы, как воздействие аддитивного теплового шума, генерируемого электронными устройствами, воздействие промышленных помех (например, автомобильные помехи от системы зажигания), воздействие атмосферных помех (электрические разряды молнии во время грозы) и т.п.
На приёмной стороне системы цифровой связи цифровой демодулятор обрабатывает искажённый каналом передаваемый сигнал и преобразует его в последовательность чисел, которые представляют оценки переданных данных (двоичных или М - позиционных). Эта последовательность чисел поступает на канальный декодер, который пытается восстановить первоначальную информационную последовательность, используя знание канального кода и избыточности, содержащейся в принятых данных.
Мера качества работы демодулятора и декодера - это частота, с которой возникают ошибки декодируемой последовательности. Более точно, средняя вероятность ошибки на бит для выходных символов декодера является удобной характеристикой качества демодулятора-декодера. Вообще говоря, вероятность ошибки является функцией от характеристик кода, форм сигналов, используемых для передачи информации по каналу, мощности передатчика, характеристик канала, а именно уровня шума, природы интерференции и т.д., и методов демодуляции и декодирования. Эти обстоятельства и их влияние на характеристики качества системы связи будут обсуждаться подробно в последующих главах.
На заключительной стадии, когда рассматривается аналоговый выход, декодер источника принимает выходную последовательность от декодера канала и, используя знание метода кодирования источника, применённого на передаче, пытается восстановить исходную форму сигнала источника. Ошибки декодирования и возможные искажения в кодере и декодере источника приводят к тому, что сигнал на выходе декодера источника является аппроксимацией исходного сигнала источника. Разность или некоторая функция разности между исходным и восстановленным сигналом является мерой искажения, внесённого цифровой системой связи.
Цифровые сигналы
Цифровой сигнал, описываемый уровнем напряжения или тока,-сигнал (импульс - для узкополосной передачи или синусоида - для полосовой передачи), представляющий цифровой символ. Характеристики сигнала (для импульсов - амплитуда, длительность и расположение или для синусоиды - амплитуда, частота и фаза) позволяют его идентифицировать как один из символов конечного алфавита. На рис. 2.2 приведен пример полосового цифрового сигнала. Хотя сигнал является синусоидальным и, следовательно, имеет аналоговый вид, все же он именуется цифровым, поскольку кодирует цифровую информацию. На данном рисунке цифровое значение указывается посредством передачи в течение каждого интервала времени Т сигнала определенной частоты.
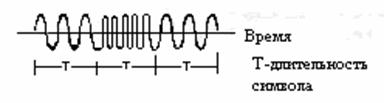
Рисунок. 1.2 - Полосовой цифровой сигнал
Скорость передачи данных. Эта величина в битах в секунду (бит/с) дается формулой R = k/T=(1/T) log2M (бит/с), где к бит определяют символ из М=2к-символьного алфавита, а Т-это длительность κ-битового символа.
Классификация сигналов. Сигнал можно классифицировать как детерминированный (при отсутствии неопределенности относительно его значения в любой момент времени) или случайный, в противном случае. Детерминированные сигналы моделируются математическим выражением x(t) = 5 cos10t. Для случайного сигнала такое выражение написать невозможно. Впрочем, при наблюдении случайного сигнала (также называемого случайным процессом) в течение достаточно длительного периода времени, могут отмечаться некоторые закономерности, которые можно описать через вероятности и среднее статистическое. Такая модель, в форме вероятностного описания случайного процесса, особенно полезна для описания характеристик сигналов и шумов в системах связи.
Периодические и непериодические сигналы. Сигнал x(t) называется периодическим во времени, если существует постоянное Т0 > 0, такое, что
x(t) =x(t + T0) для -∞<t<∞ (1.1)
где через t обозначено время. Наименьшее значение T0, удовлетворяющее это условие, называется периодом сигнала x(t). Период Тп определяет длительность одного полного цикла функции x(t). Сигнал, для которого не существует значения T0, удовлетворяющего уравнение (2.1), именуется непериодическим.
Аналоговые и дискретные сигналы. Аналоговый сигнал x(t) является непрерывной функцией времени, т.е. x(t) однозначно определяется для всех t. Электрический аналоговый сигнал возникает тогда, когда физический сигнал (например, речь) некоторым устройством преобразовывается в электрический. Для сравнения, дискретный сигнал х(кТ) является сигналом, существующим в дискретные промежутки времени; он характеризуется последовательностью чисел, определенных для каждого момента времени, кТ, где к - целое число, а T - фиксированный промежуток времени.
Сигналы, выраженные через энергию или мощность. Электрический сигнал можно представить как изменение напряжения v(t) или тока i(t) с мгновенной мощностью p{t), подаваемой на сопротивление R:
![]() (1.2)
(1.2)
Или
![]() (1.3)
(1.3)
В системах связи мощность часто нормируется (предполагается, что сопротивление 9t равно 1 Ом, хотя в реальном канале оно может быть любым). Если требуется определить действительное значение мощности, оно получается путем "денормирования" нормированного значения. В нормированном случае уравнения (2.2) и (2.3) имеют одинаковый вид. Следовательно, вне зависимости оттого, представлен сигнал через напряжение или ток, нормированная форма позволяет нам выразить мгновенную мощность как
![]() (1.4)
(1.4)
где x(t) — это либо напряжение, либо ток.
2 Лекция №2. Каналы связи и их характеристики
Цель лекции: изучение основных видов каналов связи.
Содержание:
а) понятие каналов связи;
б) проводные каналы;
в) волоконно-оптические каналы;
г) беспроводные (радио) каналы.
2.1 Понятие каналов связи
Как было указано в предшествующем обсуждении, канал связи обеспечивает соединение передатчика и приёмника. Физический канал может быть двухпроводной линией, который пропускает электрический сигнал, или стекловолокном, которое переносит информацию посредством модулированного светового луча или подводным каналом океана, в котором информация передаётся акустически, или свободным пространством, по которому несущий информационный сигнал излучается при помощи антенны.
Одна общая проблема при передаче сигнала через любой канал - аддитивный шум. Вообще говоря, аддитивный шум создаётся часто внутри различных электронных компонентов, таких, как резисторы и твёрдотельные устройства, используемые в системах связи. Эти шумы часто называют тепловым шумом. Другие источники шума и интерференции (наложения) могут возникать вне системы, например, переходные помехи от других пользователей канала.
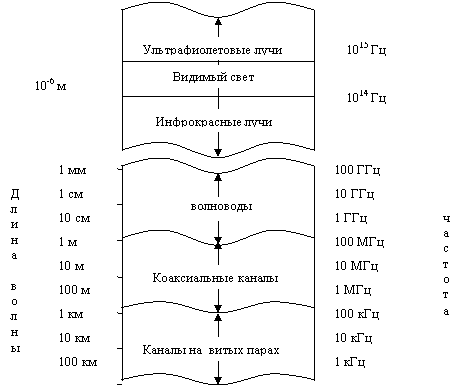
Рисунок 2.1-Частотные диапазоны для каналов связи с направляющими системами
Влияние шума может быть уменьшено увеличением мощности передаваемого сигнала. Однако конструктивные и другие практические соображения ограничивают уровень. мощности передаваемого сигнала. Другое базовое ограничение - доступная ширина полосы частот канала. Ограничение ширины полосы обычно обусловлено физическими ограничениями среды и электрических компонентов, используемых в передатчике и приемнике. Эти два обстоятельства приводят к ограничению количества данных, которые могут быть переданы надёжно по любому каналу связи. Ниже мы опишем некоторые из важных характеристик отдельных каналов связи.
2.2 Проводные каналы
Телефонная сеть экстенсивно использует проводные линии для передачи звукового сигнала, а также данных и видеосигналов. Витые проводные пары и коаксиальный кабель в основном, дают электромагнитный канал, который обеспечивает прохождение относительно умеренной ширины полосы частот. Телефонный провод, обычно используемый, чтобы соединить клиента с центральной станции, имеет ширину полосы несколько сотен килогерц. С другой стороны, коаксиальный кабель имеет обычно используемую ширину полосы частот несколько мегагерц. Рисунок 2.1 поясняет частотный диапазон используемых электромагнитных каналов, которые включают волноводы и оптический кабель.
Сигналы, передаваемые через такие каналы, искажаются по амплитуде и фазе, кроме того, на них накладывается аддитивный шум. Проводная линия связи в виде витой пары также склонна к интерференции переходных помех от рядом расположенных пар. Поскольку проводные каналы составляют большой процент каналов связи по всей стране и миру, широкие исследования были направлены на определение их свойств передачи и на уменьшение амплитудных и фазовых искажений в канале.
2.3 Волоконно-оптические каналы
Стекловолокно предоставляет проектировщику системы связи ширину полосы частот, которая на несколько порядка больше, чем у каналов с коаксиальным кабелем. В течение прошедшего десятилетия были разработаны оптические кабели, которые имеют относительно низкое затухание для сигнала и высоконадёжные оптические устройства для генерирования и детектирования сигнала. Эти технологические достижения привели к быстрому освоению таких каналов, как для внутренних систем электросвязи, так и для трансатлантических и мировых систем связи. С учётом большой ширины полосы частот, доступной на волоконно-оптических каналах, стало возможно для телефонных компаний предложить абонентам широкий диапазон услуг электросвязи, включая передачу речи, данных, факсимильных и видеосигналов.
Передатчик или модулятор в волоконно-оптической системе связи - источник света, светоизлучающий диод (СИД) или лазер. Информация передается путем изменения (модуляции) интенсивности источника света посредством сигнала сообщения. Свет распространяется через волокно как световая волна, и она периодически усиливается (в случае цифровой передачи детектируется и восстанавливается ретрансляторами) вдоль тракта передачи, чтобы компенсировать затухания сигнала.
В приемнике интенсивность света детектируется фотодиодом, чей выход является электрическим сигналом, который изменяется пропорционально мощности света на входе фотодиода. Источники шума в волоконно-оптических каналах - это фотодиоды и электронные усилители.
Предполагается, что волоконно-оптические каналы заменят почти все каналы проводной линии связи в телефонной сети на рубеже столетия.
2.4 Беспроводные (радио) каналы
В системах беспроводной связи (радиосвязи) электромагнитная энергия передается в среду распространения антенной, которая служит излучателем. Физические размеры и структура антенны зависят, прежде всего, от рабочей частоты. Чтобы получить эффективное излучение электромагнитной энергии, размеры антенны должны быть больше, чем 1/10 длины волны. Следовательно, передача радиостанции с AM на несущей, допустим, fc = 1 МГц, соответствующей длине волны λ = с/fс. = 300 м, требует антенны с диаметром, по крайней мере, 30м. Рисунок 2.2 поясняет различные диапазоны частот для радиосвязи. Способы распространения электромагнитных волн в атмосфере и в свободном пространстве можно разделить на три категории, а именно: распространение поверхностной волной, распространение пространственной волной, распространение прямой волной. В диапазоне очень низких частот (ОНЧ) и звуковом диапазоне, в которых длины волн превышают 10 км, земля и ионосфера образуют волновод для распространения электромагнитных волн. В этих частотных диапазонах сигналы связи фактически распространяются вокруг всего земного шара. По этой причине эти диапазоны частот, прежде всего, используются во всём мире для решения навигационных задач с берега до кораблей.
Ширина полосы частот канала, доступной в этих диапазонах, относительно мала (обычно составляет 1...10 % центральной частоты), и, следовательно, информация, которая передаётся через эти каналы, имеет относительно низкую скорость передачи и обычно неприемлема для цифровой передачи.
Доминирующий тип шума на этих частотах обусловлен грозовой деятельностью вокруг земного шара, особенно в тропических областях. Интерференция возникает из-за большого числа станций в этих диапазонах частот.
Распространение земной волной является основным видом распространения для сигналов в полосе средних частот (0,3...3 МГц). Это-диапазон частот, используемый для радиовещания с AM и морского радиовещания. При AM радиовещании и распространении земной волной дальность связи, даже при использовании мощных радиостанций, ограничена 150 км. Атмосферные шумы, промышленные шумы и тепловые шумы от электронных компонентов приёмника являются основными причинами искажений сигналов, передаваемых в диапазоне средних частот.
Частным случаем распространения пространственной волны является ионосферное распространение. Оно сводится к отражению (отклонение или рефракция волны) передаваемого сигнала от ионосферы, которая состоит из нескольких слоев заряженных частиц, расположенных на высоте 50...400 км от поверхности земли. В дневное время суток разогрев нижних слоев атмосферы солнцем обусловливает появление нижнего слоя на высоте ниже 120км. Эти нижние слои, особенно D-слой, вызывают поглощение частот ниже 2 МГц, таким образом, ограничивая распространения ионосферной волной радиопередач AM радиовещания. Как следствие, мощные радиовещательные сигналы с AM могут распространяться на большие расстояния посредством отражения от ионосферных слоев (которые располагаются на высоте от 140 до 400 км над поверхностью земли) и земной поверхности.
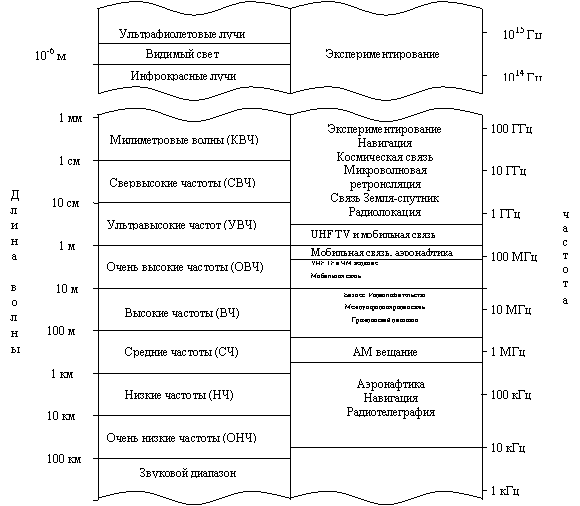
Рисунок 2.2 - Частотные диапазоны для беспроводных каналов связи
3. Лекция №3. Математические модели каналов связи
Цель лекции: изучение математических моделей каналов связи, а также рассмотрение помех в каналах связи.
Содержание:
а) математические модели каналов связи;
б) непрерывный канал;
в) дискретный канал;
г) помехи в каналах связи.
3.1 Математические модели каналов связи
При синтезе систем связи для передачи информации через физические каналы мы используем математические модели, которые отображают наиболее важные характеристики среды передачи. Затем математическая модель канала используется для синтеза кодера и модулятора в передатчике и демодулятора и декодера в приёмнике.
Канал с аддитивным шумом. Самая простая математическая модель для канала связи - это канал с аддитивным шумом, иллюстрируемый на рисунке 3.1. В этой модели передаваемый сигнал s(t) подвержен воздействию лишь аддитивного шумового процесса n(t). Физически аддитивный шум возникает от посторонних электрических помех, электронных компонентов и усилителей в приёмнике систем связи, а также из-за интерференции сигналов.
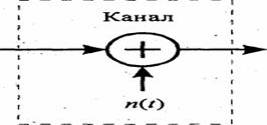
Рисунок 3.1- Канал с аддитивным шумом
Если шум обусловлен в основном электронными компонентами и усилителями в приёмнике, его можно описать как тепловой шум. Этот тип шума характеризуется статистически как гауссовский шумовой процесс. Как следствие, результирующую математическую модель обычно называют каналом с аддитивным гауссовским шумом. Поскольку эта модель применима к широкому классу физических каналов связи и имеет простую математическую интерпретацию, она является преобладающей моделью канала при анализе и синтезе систем связи. Затухание каналов легко включается в модель. Если при прохождении через канал сигнал подвергается ослаблению, то принимаемый сигнал
![]() (3.1)
(3.1)
где α- коэффициент затухания линейного канального фильтра.
Линейный фильтровой канал. В некоторых физических каналах таких, как проводные телефонные каналы, фильтры используются для того, чтобы гарантировать, что передаваемые сигналы не превышают точно установленные ограничения на ширину полосы и, таким образом, не интерферируют друг с другом. Такие каналы обычно характеризуются математически как линейные фильтровые каналы с аддитивным шумом, что иллюстрируется на рисунке 3.2. Следовательно, если на вход канала поступает сигнал s(f), на выходе канала имеем сигнал
![]() (3.2)
(3.2)
где c(f) - импульсная характеристика линейного фильтра, а * обозначает свертку.
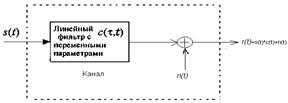
Рисунок 3.2 - Линейный фильтровой канал с аддитивным шумом
Линейный фильтровой канал с переменными параметрами. Физические каналы, такие как подводные акустические каналы и ионосферные радиоканалы, которые возникают в условиях меняющегося во времени многопутевого распространения передаваемого сигнала, могут быть описаны математически как линейные фильтры с переменными параметрами. Такие линейные фильтры характеризуются меняющимися во времени импульсной характеристикой канала c(τ,t), где с(τ,t) – отклик канала в момент времени t на 8-импульс, поданный к входу в момент t= τ.
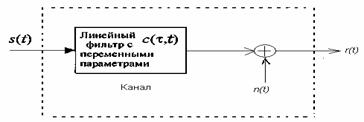
Рисунок 3.3- Линейный фильтровой канал с переменными параметрами и аддитивным шумом
Таким образом, τ представляет «ретроспективную» переменную. Линейный фильтровой канал с переменными параметрами и аддитивным шумом иллюстрируется на рисунке 3.3.
Для входного сигнала s(t) выходной сигнал канала
![]() (3.3)
(3.3)
Хорошей моделью для многопутевого распространения волн через физические каналы типа ионосферы (на частотах ниже 30 МГц) и каналы подвижной сотовой радиосвязи является частный случай (3.3), когда переменная во времени импульсная характеристика канала имеет вид
![]() (3.4)
(3.4)
где {ak(t)} определяет возможные меняющиеся во времени коэффициенты затухания для L путей распространения, {(τk.)} - соответствующие им времена задержки. Если (3.4) подставить в (3.3), то принимаемый сигнал
![]() (3.5)
(3.5)
Следовательно, полученный сигнал состоит из L компонентов распространения, где каждый компонент умножается на ak(t) и запаздывает на. τk.
Три математические модели, описанные выше, адекватно характеризуют большинство физических каналов, с которыми сталкиваются на практике. Эти три модели канала используются в книге для анализа и синтеза систем связи.
Непрерывный канал
Каналы, при поступлении на вход которых непрерывного сигнала на его выходе сигнал тоже будет непрерывным, называют непрерывными. Они всегда входят в состав дискретного канала. Непрерывными каналами являются, например, стандартные телефонные каналы связи (каналы тональной частоты - ТЧ) с полосой пропускания 0,3…3,4 кГц, стандартные широкополосные каналы с полосой пропускания 60…108 кГц, физические цепи и др. Модель канала может быть представлена в виде линейного четырехполюсника (рисунок 3.4)
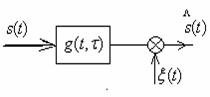
Рисунок 3.4 - Модель линейного непрерывного канала
Дискретный канал
С целью согласования кодера и декодера канала с непрерывным каналом связи используются устройства преобразования сигналов (УПС), включаемые на передаче и приеме. В частном случае - это модулятор и демодулятор. Совместно с каналом связи УПС образуют дискретный канал (ДК), т.е. канал, предназначенный для передачи только дискретных сигналов.
Дискретный канал характеризуется скоростью передачи информации, измеряемой в битах в секунду (бит/с). Другой характеристикой дискретного канала является скорость модуляции, измеряемая в бодах. Она определяется числом элементов, передаваемых в секунду.
Двоичный симметричный канал. Двоичный симметричный канал (binary symmetric channel - BSC) является частным случаем дискретного канала без памяти, входной и выходной алфавиты которого состоят из двоичных элементов (0 и I). Условные вероятности имеют симметричный вид.
![]() (3.6)
(3.6)
Уравнение (3.6) выражает так называемые вероятности перехода.
Марковские модели ДК. Состояния каналов можно различать по вероятности ошибки в каждом из состояний. Изменения вероятности ошибки можно, в свою очередь, связать с физическими причинами – появлением перерывов, импульсных помех, замираний и т.д. Последовательность состояний является простой цепью Маркова. Простой цепью Маркова называется случайная последовательность состояний, когда вероятность того или иного состояния в i-тый момент времени полностью определяется состоянием ci-1 в (i-1)-й момент. Эквивалентная схема такого канала представлена на рисунке 3.5.
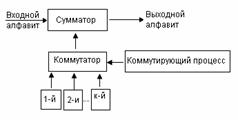
Рисунок 3.5 - Эквивалентная схема дискретного симметричного канала при описании его моделью на основе цепей Маркова
Модель Гильберта. Простейшей моделью, основанной на применении математического аппарата марковских цепей, является модель источника ошибок, предложенная Гильбертом. Согласно этой модели, канал может находиться в двух состояниях- хорошем (состояние 1) и плохом (состояние 2). Первое состояние характеризуется отсутствием ошибок. Во втором состоянии ошибки появляются с вероятностью рош (2) .
Помехи в каналах связи
В реальном канале сигнал при передаче искажается, и сообщение воспроизводится с некоторой ошибкой. Причиной таких ошибок являются искажения, вносимые самим каналом, и помехи, воздействующие на сигнал. Следует четко отделить искажения от помех, имеющих случайный характер. Помехи заранее не известны и поэтому не могут быть полностью устранены.
Под помехой понимается любое воздействие, накладывающееся на полезный сигнал и затрудняющий его прием. Помехи разнообразны по своему происхождению: грозы, помехи электротранспорта, электрических моторов, систем зажигания двигателей и т.д.
Практически в любом диапазоне частот имеют место внутренние шумы аппаратуры, обусловленные хаотическим движением носителей заряда в усилительных приборах, так называемый тепловой шум.
Классификация помех. Гармонические помехи - представляют собой узкополосный модулированный сигнал. Причинами возникновения таких помех являются снижение переходного затухания между цепями кабеля, влияние радиостанций. Импульсные помехи - это помехи, сосредоточенные по времени. Они представляют собой случайную последовательность импульсов, имеющих случайные интервалы времени, причем, вызванные ими переходные процессы не перекрываются по времени.
4 Лекция №4. Узкополосная передача
Цель лекции: изучение методов узкополосных передач и видов алфавитных кодов.
Содержание:
а) демодуляция и обнаружение;
б) обнаружение сигнала в гауссовом шуме;
в) согласованный фильтр;
г) межсимвольная интерференция;
4.1 Демодуляция и обнаружение
В течение данного интервала передачи сигнала T, бинарная узкополосная система передает один из двух возможных сигналов, обозначаемых как g1(t) и g2(t). Подобным образом бинарная полосовая система передает один из двух возможных сигналов, обозначаемых как s1(t) и s2(t). Поскольку общая трактовка демодуляции и обнаружения, по сути, совпадает для узкополосных и полосовых систем, будем использовать запись si(t) для обозначения передаваемого сигнала, вне зависимости от того, является система узкополосной или полосовой. Итак, для любого канала двоичный сигнал, переданный в течение интервала (0, Т), представляется следующим образом.
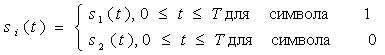 (4.11)
(4.11)
Принятый сигнал г(t) искажается вследствие воздействия шума n(t) и, возможно, неидеальной импульсной характеристики канала hc(t) и описывается следующей формулой (4.12)
![]() (4.12)
(4.12)
В нашем случае n(t) предполагается процессом AWGN с нулевым средним, а знак "*" обозначает операцию свертки, Для бинарной передачи по идеальному, свободному от искажений каналу, где свертка с функцией hc(t) не ухудшает качество сигнала (поскольку для идеального случая hc(t) - импульсная функция), вид r(t) можно упростить.
![]() i=1,2 0≤t≤T (4.13)
i=1,2 0≤t≤T (4.13)
Типичные функции демодуляции и обнаружения цифрового приемника показаны на рисунке. 4.1. Некоторые авторы используют термины "демодуляция" и "обнаружение" как синонимы. В данном конспекте они имеют различные значения. Демодуляцию (demodulation) мы определим как восстановление сигнала (в неискаженный узкополосный импульс), а обнаружение (detection) - как процесс принятия решения относительно цифрового значения этого сигнала. При отсутствии кодов коррекции ошибок на выход детектора поступают аппроксимации символов (или битов) сообщений mi’ (также называемые жестким решением). При использовании кодов коррекции ошибок на выход детектора поступают аппроксимации канальных символов (или кодированных битов) u'i , имеющие вид жесткого или мягкого решения. Для краткости термин "обнаружение" иногда применяется для обозначения совокупности всех этапов обработки сигнала, выполняемых в приемнике, вплоть до этапа принятия решении.
В блоке демодуляции и дискретизации (рисунок 4.1) изображен принимающий фильтр (по сути, демодулятор), выполняющий восстановление сигнала » качестве подготовки к следующему необходимому этапу - обнаружению. Фильтрация в передатчике и канале обычно приводит к искажению принятой последовательности импульсов, вызванному межсимвольной интерференцией, а значит, эти импульсы не совсем готовы к дискретизации и обнаружению. Задачей принимающего фильтра является восстановление узкополосного импульса с максимально возможным отношением сигнал/шум (signal-to-noise ratio - SNR) и без межсимвольной интерференции. Оптимальный принимающий фильтр, выполняющий такую задачу, называется согласованным (matched), или коррелятором (correlator).. За принимающим фильтром может находиться выравнивающий фильтр (equalizing filter), или эквалайзер (equalizer); он необходим только в тех системах, в которых сигнал может искажаться вследствие межсимвольной интерференции, введенной каналом. Принимающий и выравнивающий фильтры показаны как два отдельных блока, что подчеркивает различие их функций. Впрочем, в большинстве случаев при использовании эквалайзера для выполнения обеих функций (а следовательно, и для компенсации искажения, внесенного передатчиком и каналом) может разрабатываться единый фильтр. Такой составной фильтр иногда называется просто выравнивающим или принимающим и выравнивающим.
На рисунке 4.1 выделены два этапа процесса демодуляции/обнаружения. Этап 1, преобразование сигнала в выборку, выполняется демодулятором и следующим за ним устройством дискретизации, в конце каждого интервала передачи символа Т, на выход устройства дискретизации детекторную точку, поступает выборка z(T), иногда называемая тестовой статистикой. Значение напряжения выборки z(T) прямо пропорционально энергии принятого символа и обратно пропорционально шуму. На этапе 2 принимается решение относительно цифрового значения выборки (выполняется обнаружение). Предполагается, что шум является случайным гауссовым процессом, а принимающий фильтр демодулятора — линейным. Линейная операция со случайным гауссовым процессом дает другой случайный гауссов процесс. Следовательно, на выходе фильтра шум также является гауссовым. Значит, выход этапа 1 можно описать выражением
![]()
![]() (4.14)
(4.14)
где ![]() — желаемый компонент сигнала, а
— желаемый компонент сигнала, а ![]() — шум. Для упрощения записи выражение
(4.14) будем иногда представлять в виде z = ai+n0. Шумовой компонент n0 - это случайная гауссова переменная с нулевым средним,
поэтому z(T) — случайная гауссова переменная со средним a1 или a2, в зависимости от того, передавался
двоичный нуль или двоичная единица. Плотность вероятности случайного гауссового
шума n0 можно выразить как
— шум. Для упрощения записи выражение
(4.14) будем иногда представлять в виде z = ai+n0. Шумовой компонент n0 - это случайная гауссова переменная с нулевым средним,
поэтому z(T) — случайная гауссова переменная со средним a1 или a2, в зависимости от того, передавался
двоичный нуль или двоичная единица. Плотность вероятности случайного гауссового
шума n0 можно выразить как
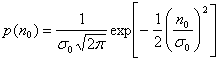 (4.15)
(4.15)
где ![]() 2 - дисперсия шума Используя выражения
(4.14) и (4.15), можно выразить плотности условных вероятностей
2 - дисперсия шума Используя выражения
(4.14) и (4.15), можно выразить плотности условных вероятностей ![]() и
и ![]() .
.
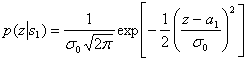 (4.16)
(4.16)
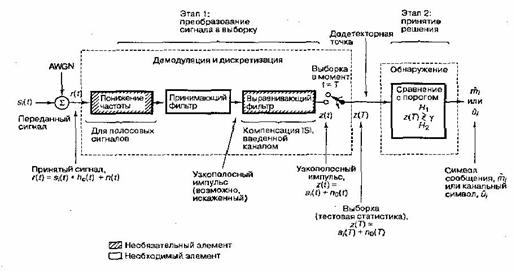
Рисунок 4.1 - Два основных этапа демодуляции/обнаружения цифровых сигналов.
4.2 Обнаружение сигнала в гауссовом шуме
Полосовая модель процесса обнаружения, рассмотренная в данной главе, практически идентична узкополосной модели, представленной в главе демодуляция и обнаружение. Дело в том, что принятый полосовой сигнал вначале преобразовывается в узкополосный, после чего наступает этап окончательного обнаружения. Для линейных систем математика процесса обнаружения не зависит от смешения частоты. Фактически теорему эквивалентности можно определить следующим образом: выполнение полосовой линейной обработки сигнала с последующим наложением сигнала (превращением полосового сигнала в узкополосный) дает те же результаты, что и наложение сигнала с последующей узкополосной линейной обработкой сигнала. Термин "наложение сигнала" (heterodyning) обозначает преобразование частоты или процесс смешивания, вызывающий смещение спектра сигнала. Как следствие теоремы эквивалентности, любая линейная модель обработки сигналов может использоваться для узкополосных сигналов (что предпочтительнее с точки зрения простоты) с теми же результатами, что и для полосовых сигналов. Это означает, что производительность большинства цифровых систем связи часто можно описать и проанализировать, считая канал передачи узкополосным.
4.3 Согласованный фильтр
Согласованный фильтр (matched filter) - это линейное устройство, спроектированное, чтобы давать на выходе максимально возможное для данного передаваемого сигнала отношение сигнал/шум. Предположим, что на вход линейного, инвариантного относительно времени (принимающего) фильтра, за которым следует устройство дискретизации (рисунок 4.2), подастся известный сигнал s(t) плюс шум AWGN n(t).
4.4 Межсимвольная интерференция
На рисунке 4.3 а) представлены фильтрующие элементы типичной системы цифровой связи. В системе - передатчике, приемнике и канале - используется множество разнообразных фильтров (и реактивных элементов, таких как емкость и индуктивность). В передатчике информационные символы, описываемые как импульсы или уровни напряжения, модулируют импульсы, которые затем фильтруются для согласования с определенными ограничениями полосы. В узкополосных системах канал (кабель) имеет распределенное реактивное сопротивление, искажающее импульсы. Некоторые полосовые системы такие, как беспроводные, являются, по сути, каналами с замираниями, которые проявляют себя как нежелательные фильтры, также искажающие сигнал. Если принимающий фильтр настраивается на компенсацию искажения, вызванного как передатчиком, так и каналом, он зачастую называется выравнивающим (equalizing filter) или принимающим/выравнивающим (receiving/equalizing). На рисунке 4.10,б приведена удобная модель системы, объединяющая следствия фильтрации в одну общесистемную передаточную функцию.
![]() (4.40)
(4.40)
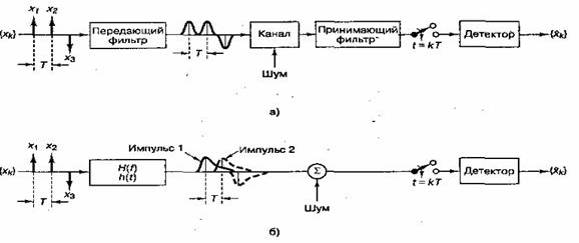
Рисунок 4.3 - Межсимвольная интерференция в процессе обнаружения:
а) типичная узкополосная цифровая система;
б) эквивалентная модель.
5. Лекция №5. Алгоритмы цифрового кодирования
Цель лекции: изучение алгоритмов цифрового кодирования и видов алфавитных кодов.
Содержание:
а) алгоритмы цифрового кодирования;
б) биполярный метод;
в) псевдотроичный метод;
г) парно-селективный троичный код.
5.1 Алгоритмы цифрового кодирования
К линейным сигналам предъявляются следующие требования:
Спектр сигнала должен быть узким и иметь ограничение как сверху, так и снизу. Чем уже спектр сигнала, тем меньше требуется полоса пропускания фотоприемника, а соответственно, уменьшаются мощность шума и его влияние. Ограничение спектра сверху снижает уровень межсимвольной помехи, а ограничение снизу – флуктуацию уровня принимаемого сигнала в электрической части фотоприемника, имеющего цепи развязки по постоянному току. Минимальное содержание низкочастотных составляющих позволяет также обеспечивать:
устойчивую работу цепи стабилизации выходной мощности оптического передатчика;
код линейного сигнала должен обеспечивать возможность выделения колебания тактовой частоты, необходимой для нормальной работы тактовой синхронизации;
код линейного сигнала должен обладать максимальной помехоустойчивостью, которая позволяет получать при прочих равных условиях максимальную длину участка регенерации;
код линейного сигнала должен обладать избыточностью, которая позволяет по нарушениям правила образования судить о возникновении ошибок;
код линейного сигнала должен быть простым для практической реализации преобразователей кода.
Для формирования линейных сигналов используется блочные коды вида nBmB, где n означает число кодируемых цифровых разрядов, B определяет двоичное основание системы счисления исходного кода, m-число передаваемых по ОВ двухуровневых сигналов, соответствующих n разрядам. Например, 1В2В обозначает, что один цифровой разряд передается двумя сигналами по ОВ и относительная скорость передачи в линейном тракте в два раза выше скорости входных символов.
Наиболее простыми линейными кодами являются так называемые NRZ – коды (без возращения к нулю) и RZ - коды (с возращением к нулю). В NRZ – коде «1» передается импульсами, а «0» - паузой (рисунок 5.1,а). В RZ – коде «1» передается последовательностью из импульса и паузой, причем, имеет в два раза меньшую длительность, а «0», как и раньше, передается паузой (рисунок 5.1,б. Недостатком кода RZ по сравнению с NRZ является необходимость использования более широкой полосы передачи из-за применения импульсов меньшей длительности, а преимуществом его является то, что источник оптического излучения в этом случае работает в течение меньшего времени и соответственно степень деградации его параметров снижается. Согласно принятому определению RZ – код является примером 1В2В – сигнала. Недостаток рассмотренных кодов заключается в том, что они не удовлетворяют перечисленным требованиям (за исключением последнего пункта), поэтому такие коды могут быть рекомендованы лишь на линиях небольшой протяженности при отсутствии регенерационных участков.
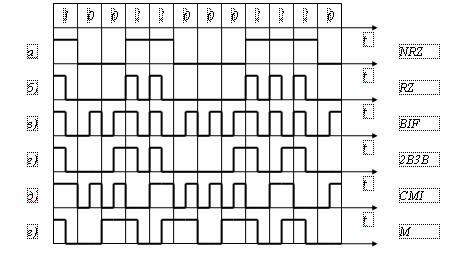
Рисунок 5.1 - Линейные коды
5.2 Биполярный метод
При биполярном методе символу 0 соответствует нулевое значение сигнала на передаче, а символу 1-попеременно значения +А или -А. В связи с этим в американской литературе его называют AMI (Alternate Mark Inversion) методом. График передаваемого сигнала показан на рисунке 4.23. Спектральная плотность мощности случайной последовательности сигналов данных относится к одному из типов, приведенных на рисунке 4.23 (кривая 2). Она обращается в нуль на нулевой частоте и на двойной частоте Найквиста 2/N. Таким образом, возможна передача и по линиям, содержащим разделительные трансформаторы. Максимум спектральной плотности прямоугольных импульсов располагается несколько ниже частоты fN.
Для восстановления информации на приеме при использовании сигналов со значениями ±АЕ и 0 пороговый уровень должен быть установлен равным ±АЕ/2.
При таком кодировании возможна только синхронная передача. Последовательность нулей преобразуется на передаче в сигнал с нулевой амплитудой, и восстановление фазы тактов в приемнике невозможно. Поэтому, чтобы сохранить синхронизм между данными и тактами на приеме, необходимо исключить появление длинных последовательностей нулей в передаваемом сигнале, например, путем скремблирования.
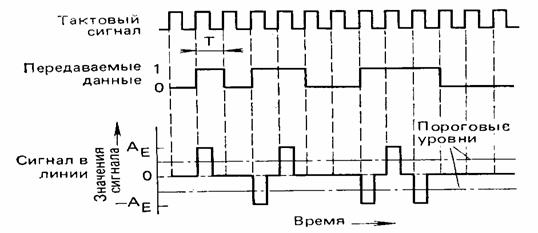
Рисунок 4.23 - Графики, иллюстрирующие биполярный метод
5.3 Псевдотроичный метод
При псевдотроичном методе прямоугольные импульсы короче тактового интервала (длительности передачи символа); например, имеют половинную длительность, и поэтому переходный процесс успевает затухнуть до того момента, когда посылается новый импульс.
Кодирование при псевдотроичном методе такое же, как и при биполярном методе, однако единица передается импульсом половинной длительности. Поэтому в американской литературе биполярный метод называют full bauded AMI-методом, а псевдотроичный - half bauded AMI-методом. Временная диаграмма показана на рис., а спектральная плотность мощности - на рисунке 5.2 (кривая 3).
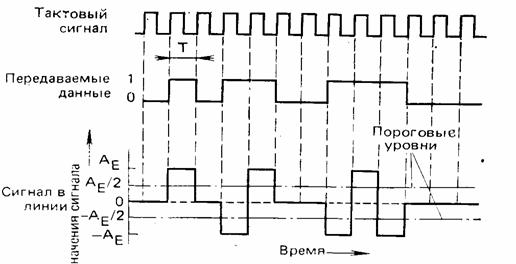
Рисунок 5.2 - Графики, иллюстрирующие псевдотроичный метод
При одинаковом пиковом напряжении на передаче высота максимума спектральной плотности значительно меньше, чем при биполярном методе; поэтому помехи, создаваемые посторонними системами, меньше, а чувствительность к помехам, напротив, больше, чем при биполярном методе. В отношении остальных свойств оба метода равноценны.
5.4 Парно-селективный троичный код
Алгоритмы замен вида BNZS, описанные в предыдущем подразделе, представляют собой примеры выбора кодов в троичном кодовом пространстве с целью увеличения содержания хронирующей составляющей двоичного сигнала. Еще одним примером является парно-селективный троичный код PST .
Процесс преобразования к коду вида PST начинается с разделения входного двоичного цифрового сигнала на пары битов с целью получения последовательностей кодовых комбинаций из двух битов. Затем эти кодовые комбинации преобразуются для передачи в два троичных символа каждая. Поскольку число двухсимвольных троичных кодовых комбинаций равно девяти, а число двухсимвольных двоичных кодовых комбинаций - только четырем, возможна значительная гибкость в выборе способа преобразования к коду передачи. Наиболее полезный из возможных форматов преобразования приведен в таблице 4.1. Этот конкретный формат не только гарантирует наличие значительной хронирующей составляющей, но и предотвращает плавание постоянной составляющей за счет переключения мод для сохранения баланса между положительными и отрицательными импульсами. Кодовые комбинации выбираются из одного столбца до тех пор, пока не будет передан одиночный импульс '. В этот момент моды в преобразователе кодов переключаются, и кодовые комбинации выбираются из другого столбца до тех пор, пока не будет передан другой одиночный импульс ' (противоположной полярности).
Таблица 5.1- Преобразование к парно-селективному троичному коду
| Двоичный входной сигнал | Мода + | Мода - |
| 00 | ─ + | ─ + |
| 01 | 0 + | 0 - |
| 10 | + 0 | - 0 |
| 11 | + ─ | + ─ |
Потенциальным недостатком алгоритма преобразования к коду PST является то, что двоичный цифровой сигнал должен быть разделен на пары. Следовательно, обратный преобразователь кода PST должен выделять границы пар. Распознавание границ не представляет труда, если передается случайный цифровой сигнал, поскольку при неправильном разбиении на пары в конце концов неизбежно образуются недопустимые кодовые комбинации (++--). Кроме того, структура циклов для временного группообразования обычно обеспечивает автоматическое получение синхронизма по кодовым комбинациям и парам.
6 Лекция №6. Полосовая модуляция и демодуляция
Цель лекции: изучение методов модуляции.
Содержание:
а) методы цифровой полосовой модуляции;
б) многопозиционная модуляция;
в) амплитудная манипуляция;
г) амплитудно-фазовая манипуляция.
6.1 Методы цифровой полосовой модуляции
Полосовая модуляция (аналоговая или цифровая) - это процесс преобразования информационного сигнала в синусоидальную волну; при цифровой модуляции синусоида на интервале Т называется цифровым символом. Синусоиды могут отличаться по амплитуде, частоте и фазе. Таким образом, полосовую модуляцию можно определить как процесс варьирования амплитуды, частоты или фазы (или их комбинаций) радиочастотной несущей согласно передаваемой информации. В общем виде несущая записывается следующим образом.
![]() (6.1)
(6.1)
Здесь A(t) — переменная во времени амплитуда, а θ(t) — переменный во времени угол. Угол удобно записывать в виде
![]() (6.2)
(6.2)
так что
![]() (6.3)
(6.3)
где ω - угловая частота несущей, а φ(t) - ее фаза. Частота может записываться как переменная f или как переменная ω. В первом случае частота измеряется в герцах (Гц), во втором - в радианах в секунду (рад/с). Эти параметры связаны следующим соотношением ω=2πf.
Если для обнаружения сигналов приемник использует информацию о фазе несущей, процесс называется когерентным обнаружением (coherent detection); если подобная информация не используется, процесс именуется некогерентным обнаружением (noncoherent detection). Вообще, в цифровой связи термины "демодуляция" (demodulation) и "обнаружение" (detection) часто используются как синонимы, хотя демодуляция делает акцент на восстановлении сигнала, а обнаружение - на принятии решения относительно символьного значения принятого сигнала. Под общим заголовком когерентной модуляции/демодуляции перечислены: фазовая манипуляция (phase shift keying - PSK), частотная манипуляция (frequency shift keying - FSK), амплитудная манипуляция (amplitude shift keying - ASK), модуляция без разрыва фазы (continuous phase modulation - CPM) и смешанные комбинации этих модуляций. Основные форматы полосовой модуляции рассмотрены в данной главе. Некоторые специализированные форматы такие, как квадратурная фазовая манипуляция со сдвигом (offset quadrature PSK - OQPSK), манипуляция с минимальным сдвигам (minimum shift keying - MSK), принадлежащие к классу модуляций СРМ, и квадратурная амплитудная модуляция (quadrature amplitude modulation - QAM).
Некогерентная демодуляция относится к системам, использующим демодуляторы, спроектированные для работы без знания абсолютной величины фазы входящего сигнала; следовательно, определение фазы в этом случае не требуется. Таким образом, преимуществом некогерентных систем перед когерентными является простота, а недостатком - большая вероятность ошибки (РЕ). Под заголовком некогерентной передачи сигналов перечислены модуляции, подобные используемым при когерентной передаче: DPSK, FSK, ASK, CPM и смешанные их комбинации. Подразумевается, что для некогерентного приема информация о фазе не используется; так почему же под заголовком "некогерентная передача" указана одна из форм фазовой манипуляции? Это вызвано тем, что одну из важных форм PSK можно отнести к некогерентной (или дифференциально - когерентной), поскольку она не требует согласования по фазе с принятой несущей.
6.2 Многопозиционная модуляция
Используя известное тригонометрическое равенство, называемое теоремой Эйлера, введем комплексную запись синусоидальной несущей
![]() (6.4)
(6.4)
Во-первых, при комплексной записи в компактной форме, ![]() указаны два
важных компонента любой синусоидальной несущей волны, называемых взаимно
ортогональными синфазной (действительной) и квадратурной (мнимой)
составляющими. Во-вторых, как показано на рисунке 6.1, не модулированная
несущая удобно представляется в полярной системе координат в виде единичного
вектора с постоянной скоростью рад/с, вращающегося против часовой стрелки.
указаны два
важных компонента любой синусоидальной несущей волны, называемых взаимно
ортогональными синфазной (действительной) и квадратурной (мнимой)
составляющими. Во-вторых, как показано на рисунке 6.1, не модулированная
несущая удобно представляется в полярной системе координат в виде единичного
вектора с постоянной скоростью рад/с, вращающегося против часовой стрелки.
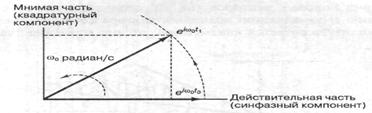
Рисунок 6.1 - Векторное представление синусоиды
При увеличении t (от t0 до t1 мы можем изобразить переменные во времени проекции вращающегося вектора на синфазной (l) и квадратурной (Q) осях. Эти декартовы оси обычно называются синфазным (l channel) и квадратурным каналом (Q channel), а их проекции представляют взаимно ортогональные составляющие сигнала, связанные с этими каналами. В-третьих, процесс модуляции несущей можно рассматривать как возмущение вращающегося вектора (и его проекций).
Рассмотрим, например, несущую, амтитудно-модулированную синусоидой с единичной амплитудой и частотой ωm, где ωm ≤ω0. Переданный сигнал имеет следующий вид.
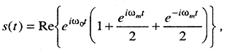 (6.5)
(6.5)
где Re{x} - действительная часть комплексной величины [х]. На рисунке
6.2 показано, что вращающийся вектор ![]() , представленный на рисунке
6.1, возмущается двумя боковыми членами -
, представленный на рисунке
6.1, возмущается двумя боковыми членами - ![]() , вращающимся против часовой
стрелки, и
, вращающимся против часовой
стрелки, и ![]() , вращающимся по часовой
стрелке. Боковые векторы вращаются намного медленнее, чем вектор несущей волны.
В результате модулированный вращающийся вектор несущей волны растет и
уменьшается согласно указаниям боковых полос, но частота его вращения остается
постоянной; отсюда и название - "амплитудная модуляция".
, вращающимся по часовой
стрелке. Боковые векторы вращаются намного медленнее, чем вектор несущей волны.
В результате модулированный вращающийся вектор несущей волны растет и
уменьшается согласно указаниям боковых полос, но частота его вращения остается
постоянной; отсюда и название - "амплитудная модуляция".
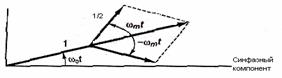
Рисунок 6.2 - Амплитудная модуляция
Еще один пример, иллюстрирующий полезность векторного представления, - это частотная модуляция (frequency modulation - FM) несущей похожей синусоидой частотой вращения ωm рад/с. Аналитическое представление узкополосной частотной модуляции (narrowband FM - NFM) подобно представлению амплитудной модуляции и описывается выражением:
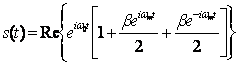 (6.6)
(6.6)
где β - коэффициент модуляции. На рисунке 6.3 показано, что, как и в предыдущем случае, вектор несущей волны возмущается двумя боковыми векторами. Но поскольку один из них, как указано в формуле (6.6), имеет знак "минус", симметрия боковых векторов, вращающихся по часовой стрелке и против нее, отличается от имеющегося случая амплитудной модуляции. При модуляции AM симметрия приводит к увеличению и уменьшению вектора несущей волны со временем. В случае модуляции NF] симметрия боковых векторов (на 90° отличающаяся от симметрии AM) приводит к ускорению и замедлению вращения вектора согласно указаниям боковых полос, при этом амплитуда остается неизменной; отсюда название - "частотная модуляция".
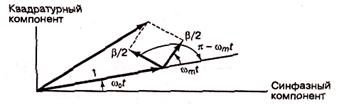
Рисунок 6.3 - Узкополосная частотная модуляция
6.3 Амплитудная манипуляция
Сигнал в амплитудной манипуляции (amplitude shift keying — ASK),
изображенной на рисунке 6.4 в, описывается выражением (6.7). На рисунке 6.4 в,
М выбрано равным 2, что соответствует двум типам сигналов. Изображенный на
рисунке сигнал в модуляции ASK
может соответствовать радиопередаче с использованием двух сигналов, амплитуды
которых равны 0 и![]() . В векторном представлении
использованы те же фазово-амплитудные полярные координаты, что и в примере для
модуляции PSK.
. В векторном представлении
использованы те же фазово-амплитудные полярные координаты, что и в примере для
модуляции PSK.
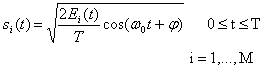 (6.7)
(6.7)
где амплитудный член ![]() может принимать М дискретных
значений, а фазовый член ф - это произвольная константа.
может принимать М дискретных
значений, а фазовый член ф - это произвольная константа.
6.4 Амплитудно-фазовая манипуляция
Амплитудно-фазовая манипуляция (amplitude phase keying - АРК) - это комбинация схем ASK и PSK. Сигнал в модуляции АРК изображен на рисунке 5.4, г и выражается как с индексированием амплитудного и фазового членов.
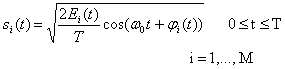 (6.8)
(6.8)
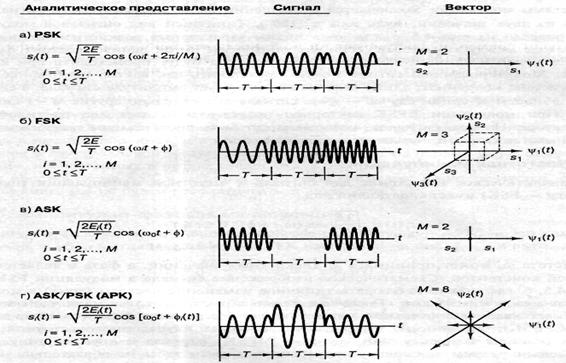
Рисунке 6.4 - Виды цифровых модуляций
7 Лекция №7. Оптимальный прием ДС сигнала
Цель лекции: изучение принципов оптимального приема ДС сигналов, векторные представление сигналов MFSK, МРSK.
Содержание:
а) оптимальный прием ДС сигнала;
б) векторное представление сигналов MFSK, МРSK.
7.1 Оптимальный прием ДС сигнала
Рассмотрим систему электросвязи для передачи дискретных сообщений (ДС).
Источник сообщений вырабатывает во времени последовательность элементов, выбираемых
из множества ![]() , где m-общее число различных элементов
множества. В зависимости от вида линии связи сообщения
, где m-общее число различных элементов
множества. В зависимости от вида линии связи сообщения ![]() предаются либо непосредственно, либо путем предварительной
модуляции переносчика. Задача приемного устройства состоит в том, чтобы на
основе анализа реализаций принятого сигнала вынести решение: какой передавался
сигнал. При этом следует иметь в виду, что полностью безошибочное решение
невозможно.
предаются либо непосредственно, либо путем предварительной
модуляции переносчика. Задача приемного устройства состоит в том, чтобы на
основе анализа реализаций принятого сигнала вынести решение: какой передавался
сигнал. При этом следует иметь в виду, что полностью безошибочное решение
невозможно.
Решение, соответствующее некоторому критерию оптимальности, называют оптимальным решением, а приемник, работающий в соответствии с таким критерием, - оптимальным приемником.
На рисунке 5.5 для случайной переменной z(T) показаны две
плотности условных вероятностей - ![]() — со средними значениями а,
и а2. Эти функции именуются правдоподобием s1, и правдоподобием s2. Приведем
их .
— со средними значениями а,
и а2. Эти функции именуются правдоподобием s1, и правдоподобием s2. Приведем
их .
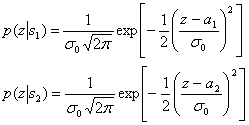 (7.1)
(7.1)
Здесь σ02 - дисперсия шума. На рисунке 7.1 правое правдоподобие p(z│s1) иллюстрирует вероятностное распределение сигналов на выходе детектора z(T) при переданном сигнале s1.
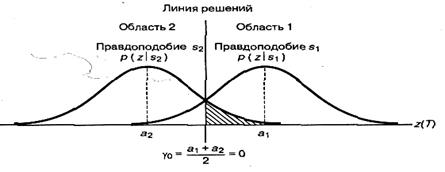
Рисунок 7.1 - Плотность условных вероятностей
Подобным образом левое правдоподобие p(z│s2) демонстрирует вероятностное распределение сигналов на выходе детектора г(Т) при переданном сигнале s2. Абсцисса z(Г) представляет полный диапазон возможных значений выборок на выходе корреляционного приемника, показанного на рисунке 7.2.
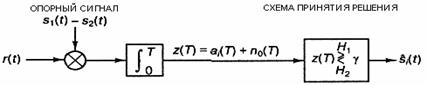
Рисунок 7.2 - Двоичный корреляционный приемник
При рассмотрении задачи оптимизации порога двоичного решения относительно принадлежности принятого сигнала к одной из двух областей было показано, что критерий минимума ошибок для равновероятных двоичных сигналов, искаженных гауссовым шумом, можно сформулировать следующим образом
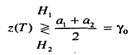 (7.2)
(7.2)
Здесь а1 - сигнальный компонент z(T) при передаче s1(t), а а2 - сигнальный компонент z(Т) при передаче s2(t). Порог γ0, равный (а1+а2)/2, - это оптимальный порог для минимизации вероятности принятия неверного решения при равновероятных сигналах и симметричных правдоподобиях. Правило принятия решения, приведенное в формуле (7.2), указывает, что гипотеза H1, (решение, что переданный сигнал - это s1(t) выбирается при z(T) >γ0. а гипотеза Н2 (решение, что переданный сигнал - это s2(t) - при z(T) < γ0 Если z(T) = γ. Решение может быть любым. При равновероятных антиподных сигналах с равными энергиями, где s1(t) = - s2(t) и а1=-а2, оптимальное правило принятия решения принимает следующий вид.
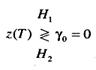 (7.3)
(7.3)
7.2.1 Векторное представление сигналов MFSK (многочаcтотная фазовая манипуляция)
Поскольку сигнальное пространство MFSK описывается М взаимно перпендикулярными осями, мы без труда можем проиллюстрировать случаи М=2 и М = 3. Итак, на рисунке 7.3, а видим бинарные ортогональные векторы s1 и s2.
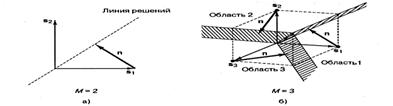
Рисунок 7.3 - Наборы сигналов для MFSK для М=2,3
На рисунке 7.3, б - показано трехмерное сигнальное пространство со взаимно перпендикулярными координатными осями. В этом случае плоскости решений разбивают пространство на три области. Показано, как к каждому сигнальному вектору s1, s2 и s3 прибавляется вектор шума n, представляющий минимальный вектор, который может привести к принятию неправильного решения. Векторы шума на рисунке 7.3, б имеют тот же модуль, что и вектор шума, показанный на рисунке 7.3, a. При данном уровне принятой энергии расстояние между любыми двумя векторами сигналов-прототипов si и sj-М-мерного ортогонального пространства является константой. Отсюда следует, что минимальное расстояние между вектором сигнала-прототипа и любой границей решений не меняется с изменением М. В отличие от модуляции MPSK, когда добавление нового сигнала к сигнальному множеству делало сигналы более уязвимыми к меньшим векторам шума, при MFSK такого не происходит.
Для иллюстрации этого момента можно было бы нарисовать ортогональные пространства высших размерностей, но, к сожалению, это затруднительно. Мы можем использовать только наш «мысленный взгляд», чтобы понять, что увеличение сигнального множества М путем введения дополнительных осей, причем, каждая новая ось перпендикулярна всем существующим, не приводит к его уплотнению. Следовательно, переданный сигнал, принадлежащий ортогональному набору, не становится более уязвимым к шуму при увеличении размерности.
Пониманию улучшения надежности при ортогональной передаче сигналов способствует сравнение зависимости вероятности символьной ошибки (РЕ) от ненормированного отношения сигнал/шум (signal-to-noise ratio — SNR) с зависимостью РЕ от Eb/N0. Стоит отметить, что изучение зависимости достоверности передачи от M при фиксированном SNR не является лучшим направлением в цифровой связи. Фиксированное SNR означает фиксированный объем энергии на символ; следовательно, при увеличении М этот объем энергии необходимо распределять уже между большим числом битов, т.е. на каждый бит приходится меньше энергии. В этой связи наиболее удобным способом сравнения различных цифровых систем является использование в качестве критерия отношения сигнал/шум, нормированного на бит, или Eb/N0. Повышение достоверности передачи с увеличением М проявляется только в том случае, если вероятность ошибки изображается как зависимость от Eb/N0. В этом случае при увеличении М отношение Eb/N0, требуемое для получения заданной вероятности ошибки, снижается при фиксированном SNR; следовательно, нам нужен новый график, где ось абсцисс представляет не SNR, a Eb/N0.
7.2.2 Векторное представление сигналов MPSK (многофазовая манипуляция). На рисунке 7.4 показаны наборы сигналов MPSK для М = 2, 4, 8 и 16. На рисунке 7.4, а видим бинарные (к=1, М = 2) антигодные векторы S1 и s2, угол между которыми равен 180°. Граница областей решений разделяет сигнальное пространство на две области. На рисунке также показан вектор шума n, равный по амплитуде сигналу S1,. При указанных направлении и амплитуде энергия вектора шума является минимальной, и детектор может допустить символьную ошибку.
На рисунке 7.4, б видим 4-арные (k = 2, М = 4) векторы, расположенные друг к другу под углом 90°. Границы областей решений (на рисунке изображена только одна) делят сигнальное пространство на четыре области.
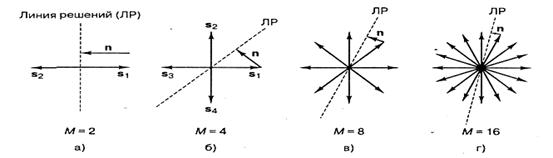
Рисунок 7.4 - Наборы сигналов MPSK для М=2,4,8,16
Здесь также изображен вектор шума n (начало — в вершине вектора сигнала, направление перпендикулярно ближайшей границе областей решений), являющийся вектором минимальной энергии, достаточной, чтобы детектор допустил символьную ошибку. Отметим, что вектор шума минимальной энергии на рисунке 7.4, б меньше вектора шума на рисунке 7.4 а, что свидетельствует о большей уязвимости 4-арной системы к шуму по сравнению с бинарной (энергии сигналов в обоих случаях взяты равными). Изучая рисунок 7.4, в, г, можно отмстить следующую закономерность. При многофазной передаче сигналов по мере роста величины М на сигнальную плоскость помещается все больше сигнальных векторов. По мере того как векторы располагаются плотнее, для появления ошибки вследствие шума требуется все меньше энергии.
С помощью рисунка 7.4 можно лучше понять поведение зависимости вероятности РB от Eb/N0, при росте к. Кроме того, рисунок позволяет взглянуть на природу компромиссов при многофазной передаче сигналов. Размещение большего числа векторов сигналов в сигнальном пространстве эквивалентно повышению скорости передачи данных без увеличения системной ширины полосы (все векторы ограничиваются одной и той же плоскостью). Другими словами, мы повысили использование полосы за счет вероятности ошибки. Рассмотрим рисунок 7.4, г, где из приведенных вариантов вероятность ошибки является наивысшей. Чем мы может заплатить, чтобы "выкупить" возросшую вероятность ошибки? Иными словами, чем мы можем поступиться, чтобы расстояние между соседними векторами сигналов на рисунке 7.4, д стало таким же, как на рисунке 7.4, а, Отметим, что на схемах, изображенных на рисунке 7.4, а для различных значений М, все векторы имеют одинаковую амплитуду. Это равносильно утверждению, что сопоставление различных схем выполняется при фиксированном отношении Es/N0, где Es - энергия символа.
8 Лекция №8. Спектральные характеристики модулированных колебаний
Цель лекции: изучение спектральных характеристик модулированных колебаний, оптимального приемника.
Содержание:
а) спектральные характеристики модулированных колебаний;
б) оптимальный приемник;
в) когерентный и некогерентный прием;
г) цифровой согласованный фильтр.
8.1 Спектральные характеристики модулированных колебаний
Остановимся на наиболее часто встречающемся случае, когда, в качестве несущей используется гармоническое колебание вида
![]() (8.1)
(8.1)
Где ![]() -амплитуда, частота и фаза
несущей.
-амплитуда, частота и фаза
несущей.
Воздействуя на тот или иной параметр несущей (![]() ), получаем
амплитудную, частотную или фазовую модуляцию. Все это-методы преобразования
исходного (модулирующего спектра частот) первичного сигнала, позволяют
обеспечить передачу информации по каналу связи с характеристиками типа
полосового фильтра. Перенос спектра, реализуемый в процессе модуляции,
позволяет также решить задачу построения многоканальных систем с ЧРК.
), получаем
амплитудную, частотную или фазовую модуляцию. Все это-методы преобразования
исходного (модулирующего спектра частот) первичного сигнала, позволяют
обеспечить передачу информации по каналу связи с характеристиками типа
полосового фильтра. Перенос спектра, реализуемый в процессе модуляции,
позволяет также решить задачу построения многоканальных систем с ЧРК.
Модулированный по амплитуде сигнал содержит в своем составе спектральные
составляющие с частотами ![]() . Составляющие с частотами
. Составляющие с частотами ![]() называются
соответственно нижней и верхней полосой АМ сигнала. Спектр АМ сигнала в 2 раза
шире спектра исходного моделирующего сигнала.
называются
соответственно нижней и верхней полосой АМ сигнала. Спектр АМ сигнала в 2 раза
шире спектра исходного моделирующего сигнала.
Частотная модуляция является другим способом переноса спектра первичного сигнала в заданный диапазон частот, но в отличие от АМ, этот способ преобразования является нелинейным. Спектр ЧМ сигнала может быть представлен как суперпозиция спектров двух АМ сигналов, один из которых имеет несущую f1, а второй f2. Из этого следует, что ширина спектра ЧМ сигнала шире, чем у АМ сигнала на величину, определяемую расстоянием между несущими f1 и f2. Значение Δf=(f1 - f2)/2 характеризует изменение частоты при передаче 1(0) относительно ее среднего значения и называется девиацией частоты.
8.2 Оптимальный приемник
Предполагается, что сигнал искажается только вследствие шума AWGN. Принятый сигнал будем описывать как сумму переданного сигнала и случайного шума.
![]() (8.2)
(8.2)
При наличии подобного принятого сигнала процесс обнаружения включает два основных этапа. На первом этапе принятый сигнал г(t) усекается до одной случайной переменной z(T) или до набора случайных переменных zi(T) (i= 1, ..., М), формируемых на выходе демодулятора и устройства дискретизации в момент времени t = T, где Т - длительность символа. На втором этапе на основе сравнения z(T) с порогом или согласно критерию максимума zi(T) принимается решение относительно значения символа. Вообще, этап 1 можно рассматривать как преобразование сигнала в точку в пространстве решений. Эту точку, представляющую собой важнейшую контрольную точку в приемнике, можно назвать додетекторной (predetection). В каждый момент передачи символа сигнал, доступный в додетекторпой точке, является выборкой узкополосного импульса. На данный момент битового значения у нас еще нет.
Cогласованный фильтр обеспечивает максимальное отношение сигнал/шум на выходе фильтра в момент t = T. Как одна из реализаций согласованного фильтра описывался коррелятор. Теперь мы можем определит корреляционный приемник, состоящий, как показано на рисунке 8.1 а, из М корреляторов, выполняющих преобразование принятого сигнала r(t) в последовательность М чисел или выходов коррелятора, zi(T) (i= 1,..М). Каждый выход коррелятора описывается следующим интегралом произведения или корреляцией с принятым сигналом.
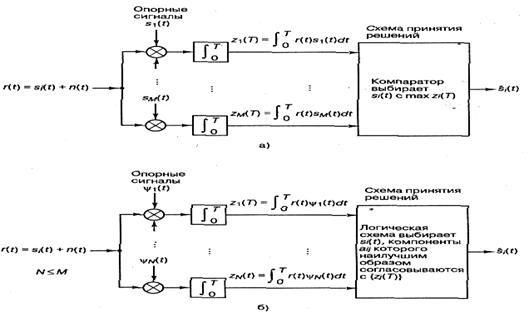
Рисунок 8.1- Корреляционный приемник
8.3 Когерентный и некогерентный прием
На рисунке 8.1,б показан детектор, который может использоваться для когерентного обнаружения любого цифрового сигнала. Подобный корреляционный детектор часто называется детектором, работающим по критерию максимального правдоподобия (maximum likelihood detector).
Вообще, схема DPSK менее эффективна, чем PSK, поскольку в первом случае вследствие корреляции между сигналами, ошибки имеют тенденцию к распространению (на соседние времена передачи символов). Стоит помнить, что схемы PSK и DPSK отличаются тем, что в первом случае сравнивается принятый сигнал с идеальным опорным, а во втором — два зашумленных сигнала. Отметим, что модуляция DPSK дает вдвое больший шум, чем модуляция PSK. Следовательно, при использовании DPSK следует ожидать вдвое (на 3 дБ) большей вероятности ошибки, чем в случае PSK; ухудшение качества передачи происходит довольно быстро с уменьшением отношения сигнал/шум. Преимуществом схемы DPSK можно назвать меньшую сложность системы.
8.4 Цифровой согласованный фильтр
Особенность согласованного фильтра - то, что его импульсная характеристика представляет собой запаздывающую версию зеркального отображения (поворота относительно оси t = 0) входного сигнала.
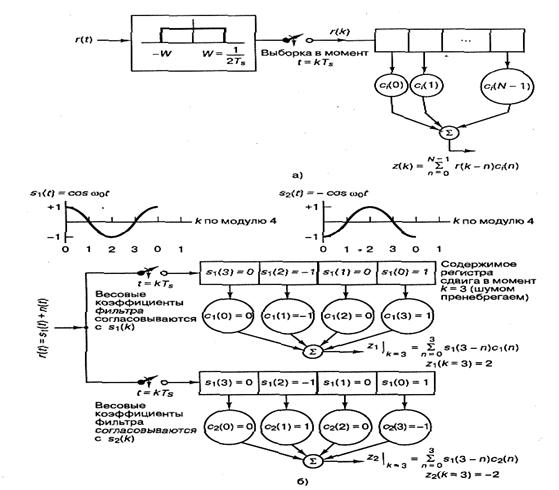
Рисунок 8.2 - Цифровой согласованный фильтр:
а) дискретный согласованный фильтр;
б) пример обнаружения с использованием дискретного согласованного фильтра.
На рисунке 8.2, б, где сигналы-прототипы изображены как функции времени, видим, что крайняя слева выборка (амплитуда, равная +1 графика) s1(t) представляет выборку в момент времени к = 0. Предполагая, что передан был сигнал s1(t) и для упрощения записи мы пренебрегли шумом, можем записать принятую выборку r(к) как s1(t). Выборки заполняют разряды согласованного фильтра, и в конце каждого периода передачи символа в крайнем правом разряде каждого регистра расположена выборка к = 0. По этой причине коррелятор можно реализовать как согласованный фильтр.
На рисунке 8.2, б обнаружение, происходящее после выхода сигнала с согласованного фильтра, осуществляется обычным образом. Для принятия двоичного решения выходы Zi(k) изучаются при каждом значении k=N-l, соответствующем концу символа.
8.5 Оценка помехоустойчивости модулированных сигналов
В таблице 8.1 и на рис.8.3 приведены аналитические выражения и графики Рв для наиболее распространенных схем модуляции, описанных выше.
Т а б л и ц а 8.1 - Вероятность ошибки для различных бинарных модуляций
| Модуляция |
РВ |
| PSK (когерентное обнаружение) |
|
| DPSK (дифференциальное когерентное обнаружение) |
|
| Ортогональное FSK (когерентное обнаружение) |
|
| Ортогональное PSK (некогерентное обнаружение) |
|
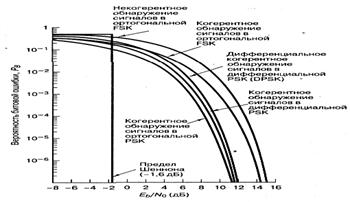
Рисунок 8.3 - Вероятность появления ошибочного бита для бинарных систем нескольких типов
9 Лекция №9. Методы синхронизации в ЦСС
Цель лекций: изучение методов синхронизации в ЦСС.
Содержание:
а) синхронизация в синхронных и асинхронных системах;
б) синхронизация поэлементная, групповая и цикловая;
в) когерентный и некогерентный прием;
г) цифровой согласованный фильтр.
9.1 Синхронизация в синхронных и асинхронных системах
При синхронном методе передачи передатчик непрерывно формирует элементы сигнала длительностью τ0, равной единичному интервалу элементы объединяются в комбинации длительностью Тк. Зная момент начала включения передатчика t0, можно определить время прихода единичного элемента, а зная число единичных элементов кодовой комбинации, легко отделить одну кодовую комбинацию от другой. На рисунке 9.2, б, в показаны соответственно импульсы отделяющие один элемент от другого и одну группу элементов от другой. Определив интервалы времени, на которых появляются элементы, можно предсказать время прихода наиболее устойчивой части элементов сигнала. Регистрируя сигнал в этой части, можно снизить вероятность неправильного приема элемента.
Синхронная работа распределителя передатчика и приемника обычно поддерживается автоматически. Для этого в приемнике по мере необходимости вырабатываются сигналы подстройки частоты задающего генератор (ЗГ) приема. Частота этого генератора должна по возможности совпадать с частотой генератора передачи. Пусть частота ЗГ fзп на передачи равна номинальной fн. Частота ЗГ на приеме вследствие нестабильности может отклоняться от номинального значения fн на величину Δf (коэффициент нестабильности k= Δf/ fн). Уход частоты ЗГ на приеме приводит к отклонению тактовой последовательности от ее идеального положения, причем, со временем расхождения по фазе будет накапливаться. Пусть в момент t0=0 тактовая последовательность совпадает с идеальной. Определим время, за которое уход по фазе в полях от длительности единичного элемента будет равен величине ε. Для этого рассмотрим два гармонических сигнала с частотами f1 и f2, вырабатываемых соответственно ЗГ на передаче и приеме (рисунок 9.1). Из этих колебаний формируется тактовая последовательность (последовательность синхроимпульсов).
Пусть f1=1/(Т-ΔТ), где Т= τ0, f2=1/(Т+ΔТ). За τ0/ ΔТ=n единичных интервалов расхождение по фазе достигнет ε=1. Это произойдет за время
![]() (9.1)
(9.1)
где κ= ΔТ/ τ0 или с учетом относительной нестабильности генератора передатчика и приемника tε=1/2κВ.
Если обозначить допустимое расхождение по фазе через εдоп, то время, за которое уход по фазе будет превышать допустимое значение (произойдет рассинхронизация),
![]() (9.2)
(9.2)
Если εдоп выразить в процентах от единичного элемента, то формула (9.2) примет вид
![]() (9.3)
(9.3)
Используя полученное выражение, можно также для заданных tε доп и В определить необходимую величину κ.
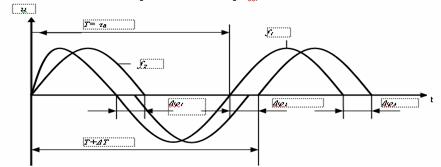
Рисунок 9.1 - Гармонические сигналы задающих генераторов передачи и приема
9.2 Синхронизация поэлементная, групповая и цикловая
Синхронизация есть процесс установления и поддержания определенных временных соотношений между двумя и более процессами. Различают поэлементную, групповую и цикловую синхронизацию. В соответствии с ГОСТ 17657–79 поэлементная, групповая и цикловая синхронизация - это синхронизация переданного и принятого цифровых сигналов данных, при которой устанавливаются и поддерживаются требуемые фазовые соотношения между значащими моментами переданных и принятых соответственно единичных элементов сигналов, групп единичных элементов этих сигналов и циклов их временного объединения. Поэлементная синхронизация позволяет на приеме правильно отделить один единичный элемент от другого и обеспечить наилучшие условия для его регистрации. Групповая синхронизация обеспечивает правильное разделение принятой последовательности на кодовые комбинации, а цикловая синхронизация - правильное разделение циклов временного объединения элементов на приеме. Обычно задачи цикловой и групповой синхронизации решаются одними и теми же методами.
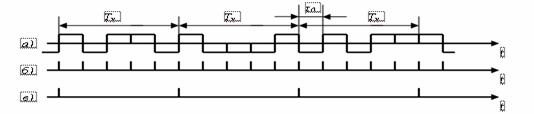
Рисунок 9.2 - Формирование элементов кодовой комбинации при синхронном методе передачи
Рассмотрим особенности поэлементной и групповой синхронизации стартстопных систем.
Устройства и принцип работы синхронизации по элементам. К устройствам синхронизации по элементам предъявляются следующие требования:
1. Высокая точность синхронизации. Допустимое относительное отклонение синхроимпульсов (тактовых импульсов) от моментов, соответствующих идеальной синхронизации, εдоп= ± 3%.
2. Малое время вхождения в синхронизм как при первоначальном включении, так и после перерыва связи.
3. Сохранение синхронизма при наличии помех и кратковременных перерывов связи.
4. Независимость точности синхронизации от статической структуры передаваемого сообщения.
Указанные требования противоречивы. Однако путем выбора рациональной структуры сигналов и выбора оптимальных параметров устройств синхронизации можно обеспечить требуемую точность синхронизации.

Рисунок 9.3 -Структурная схема резонансного устройства поэлементной синхронизации
Замкнутые устройства поэлементной синхронизации. Замкнутые устройства синхронизации широко используются в низко- и среднескоростных системах связи.
Замкнутые устройства синхронизации разделяются на два подкласса: с непосредственным воздействием на задающий генератор синхроимпульсов и с косвенным воздействием.
Упрощенная структурная схема замкнутого устройства синхронизации изображена на рисунке 9.4.
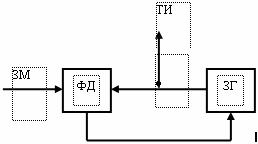
Рисунок 9.4 - Структурная схема замкнутого устройства синхронизации
Фазовое рассогласование. В фазовом дискриминаторе ФД осуществляется сравнение по фазе значащих моментов ЗМ принимаемого сигнала с тактовыми импульсами (ТИ), вырабатываемыми ЗГ. При расхождении по фазе вырабатывается управляющий сигнал, меняющий частоту ЗГ. При этом если ТИ появляются позже ЗМ (ЗГ «отстает»), то частота ЗГ увеличивается. Если ТИ появляются раньше ЗМ (ЗГ «спешит»), то частота ЗГ уменьшается.
Устройства синхронизации с непосредственным воздействием на частоту генераторов по способу управления делится на две группы:
Устройство с дискретным (релейным) управлением, в которых управляющее устройство дискретно изменяет управляющий сигнал время от времени. В интервалах между подстройками управляющий сигнал остается постоянным и зависит от величины расхождения по фазе;
Структурная схема устройства синхронизации с дискретным управлением приведена на рисунке 9.5, а его временная диаграмма – на рис. 9.6. На фазовый дискриминатор, содержащий формирователь фронтов ФФ, инвертор и логические схемы И1, И2, поступают одновременно два сигнала: информационные сигналы в виде ЗМ и тактовые импульсы. Задающий генератор с помощью преобразователя сигнала, который преобразует гармонический сигнал с выхода генератора в прямоугольный сигнал, вырабатывает серию тактовых импульсов (рисунок 9.6, в).
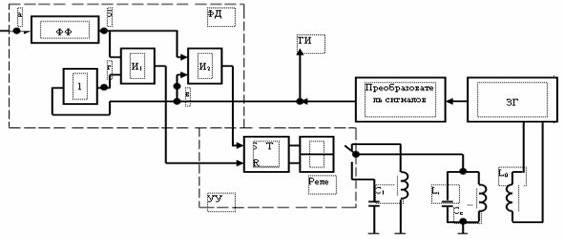
Рисунок 9.5 - Структурная схема устройства синхронизации с дискретным управлением
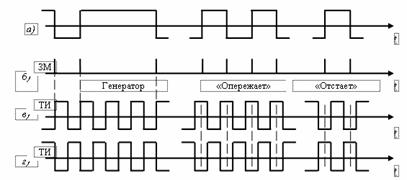
Рисунок 9.6 - Временная диаграмма работы резонансного устройства поэлементной синхронизации
10 Лекция №10. Методы и устройства помехоустойчивого кодирования
Цель лекции: изучение принципов помехоустойчивого кодирования
Содержание:
а) основные принципы обнаружения и исправления ошибок;
б) кодовое расстояние и корректирующая способность кода;
в) классификация корректирующих кодов.
10.1 Основные принципы обнаружения и исправления ошибок
Рассмотрим два основных метода использования избыточности для защиты от ошибок. В первом методе, обнаружение ошибок и повторная передача, для проверки на наличие ошибки используется контрольный бит четности (дополнительный бит, присоединяемый к данным). При этом приемное оконечное устройство не предпринимает попыток исправить ошибку, оно просто посылает передатчику запрос на повторную передачу данных. Следует заметить, что для такого диалога между передатчиком и приемником необходима двухсторонняя связь. Второй метод, прямое исправление, требует лишь односторонней линии связи, поскольку в этом случае контрольный бит четности служит как для обнаружения, так и исправления ошибок. Далее мы увидим, что не все комбинации ошибок можно исправить, так что коды коррекции классифицируются в соответствии с их возможностями исправления ошибок.
Принцип обнаружения и исправления ошибок кодами хорошо иллюстрируется с помощью геометрических моделей. Любой n- элементный двоичный код можно представить n – мерным кубом, в котором каждая вершина отображает кодовую комбинацию, а длина ребра куба соответствует одной единице. В таком кубе расстояние между вершинами измеряется минимальным количеством ребер, находящихся между ними, обозначается d и называется кодовым расстоянием.
10.2 Кодовое расстояние и корректирующая способность кода
Кодовое расстояние – это минимальное число элементов, в которых любая кодовая комбинация отличается от другой ( по всем парам кодовых слов). Например, код состоит из комбинаций 1011, 1101, 1000, и 1100. Сравнивая первые две комбинации, путем сложения их по модулю 2 находим, что d=2. Наибольшее значение d=3 получается при сравнении первой и четвертой комбинации, а наименьшее d=1 – второй и четвертой, третьей и четвертой комбинации. Выберем в трехмерном кубе такие вершины, кодовые обозначения которых отличались бы друг от друга на d=3. Такие вершины расположены на концах пространственных диагоналей куба. Их может быть только четыре пары: 000 и 111, 001 и 110, 100 и 011, 010 и 101. Код, образованный по такому правилу, может исправить одиночную ошибку или обнаружить две одиночные ошибки.
Корректирующая способность кода зависит от кодового расстояния: а) при d=1 ошибка не обнаруживается; б) при d=2 обнаруживаются одиночные ошибки; в) при d=3 исправляются одиночные ошибки или обнаруживаются двойные ошибки. В общем случае
![]() (10.1)
(10.1)
где d- минимальное кодовое расстояние, r- число обнаруживаемых ошибок, s- число исправляемых ошибок. При этом обязательным условием является r≥s.
10.3 Классификация корректирующих кодов
Корректирующими называются коды, позволяющие обнаружить и исправить ошибки в кодовых комбинациях. Они делятся на две группы: 1) коды с обнаружением ошибок; 2) коды с обнаружением и исправлением ошибок.
1) Особенность кодов с обнаружением ошибок состоит в том, что кодовые комбинации, входящие в их состав, отличаются друг от друга не менее, чем на d=2. Их можно условно разделить на две группы:
а) коды, построенные путем уменьшения числа используемых комбинаций.
Код с постоянным числом единиц и нулей в комбинациях (код с постоянным весом).
![]() (10.2)
(10.2)
где l – число единиц в слове длиной n.
Распределительный код ![]() Это также разновидность кода с
постоянным весом, равным единице. В любой кодовой комбинации содержится только
одна единица. Число кодовых комбинаций в распределительном коде
Это также разновидность кода с
постоянным весом, равным единице. В любой кодовой комбинации содержится только
одна единица. Число кодовых комбинаций в распределительном коде
![]() (10.3)
(10.3)
Кодовые комбинации при n=6 можно записать в виде 000001,000010,000100,001000,010000,100000. Сложение по модулю 2 двух комбинаций показывает, что они отличаются друг от друга на кодовое расстояние d=2.
Т а б л и ц а 10.1 - Код с постоянным числом единиц и нулей
|
Код |
Код |
|
11000 10010 01010 00011 01100 01001 00101 10001 00110 10100 |
1010100 0101010 1110000 0000111 1001001 |
б) коды, в которых используются все комбинации но к каждой из них по определенному правилу добавляются контрольные символы m - символы.
Код с проверкой на четность. Такой код образуется путем добавления к передаваемой комбинации, состоящей из к информационных символов неизбыточного кода, одного контрольного символов m (0 или 1), так, чтобы общее число единиц в передаваемой комбинации было четным. В общем случае
![]() (10.4)
(10.4)
Т а б л и ц а 10.2 - Код с проверкой на четность
|
Информационные символы к |
Контрольные символы m |
Полная кодовая комбинация n=k+m |
| 1 | 2 | 3 |
|
11011 10101 00010 11000 11110 11111 |
0 1 1 0 0 1 |
110110 101011 000101 110000 111100 111111 |
Общее число комбинаций N=2n-1
Код с числом единиц, кратным трем. Этот код образуется добавлением к к информационным символам двух дополнительных контрольных символов (m=2), имеющих такие значения, чтобы сумма единиц, посылаемых в линию кодовых комбинаций, была кратной трем
Т а б л и ц а 10.3
|
Информационные символы к |
Контрольные символы m | Полная кодовая комбинация |
|
000110 100011 101011 |
10 00 11 |
00011010 10001100 10101111 |
2) Особенность кодов с обнаружением ошибок в том, что они образуют корректирующий код, который позволяет не только обнаруживать, но и исправлять ошибки. Составление корректирующих кодов производят по следующему правилу: сначала определяют количество контрольных символов, которое следует добавить к данной кодовой комбинации, состоящей из информационных символов. Далее устанавливают место, где эти контрольные символы должны быть расположены и их состав. На приеме обычно делают проверку на четность определенной части разрядов.
Коды Хемминга. Коды Хэмминга (Hamming codes) — это простой класс блочных кодов, которые имеют следующую структуру:
![]() (10.4)
(10.4)
где m= 2,3,..Минимальное расстояние этих кодов равно 3, поэтому они способны исправлять вес однобитовые ошибки или определять все ошибочные комбинации из двух или менее ошибок в блоке. Декодирование с помощью синдромов особенно хорошо подходит к кодам Хэмминга. Фактически синдром можно превратить в двоичный указатель местоположения ошибки. Хотя коды Хэмминга не являются слишком мощными, они принадлежат к очень ограниченному классу блочных кодов, называемых совершенными.
Циклические коды. Важным подклассом линейных блочных кодов являются двоичные циклические коды (cyclic codes). Код легко реализуется на регистре сдвига с обратной связью; на подобных регистрах сдвига с обратной связью вычисляется синдром; алгебраическая структура циклического кода естественным образом позволяет эффективно реализовать методы декодирования. Итак, линейный код (n, к) называется циклическим, если он обладает следующим свойством. Если n-кортеж U= (u0, u1, и2, …, un-1) является кодовым словом в подпространстве S, тогда U(1)= (un-1, u0, u1, и2,..., un-1), полученный из U с помощью циклического сдвига, также является кодовым словом в S. Или, вообще, U(i) = (un-i;. un-i+1,…, un-1, u0, u1,… un-i-1), полученный i циклическими сдвигами, является кодовым словом в S.
Циклический код Файра. Циклические коды, обнаруживающие и исправляющие пакеты ошибок (коды Файра). Под пакетом ошибок длиной b понимают такой вид комбинации помехи, в которой между крайними разрядами, пораженными помехами, содержится b-2 разряда. Например, при b=5 комбинации помехи, т.е. пакет ошибок, могут иметь следующий вид: 10001 (поражены тоько два крайних символа), 11111 (поражены все символы), 10111, 11101, 11011 (не поражен лишь один символ), 10011, 11001, 10101 (поражены три символа). При любом варианте непременным условием пакета данной длины является поражение крайних символов.
Коды Файра могут исправлять пакет ошибок длиной b и обнаруживать пакет ошибок длиной b [заметим, что в кодах Файра понятие кодового расстояния - d].
Коды Боуза-Чоудхури-Хоквингэма.![]() . Эти коды, разработанные
Боузом, Чодхури и Хоквинхемом (сокращенно коды БЧХ), позволяют обнаруживать и
исправлять любое число ошибок. Заданными при кодировании является число ошибок s, которое следует исправить, и общее
число символов, посылаемых в линию, т.е. длина слов n. Числа информационных символов k и контрольных символов m, а также состав контрольных символов подлежат определению.
. Эти коды, разработанные
Боузом, Чодхури и Хоквинхемом (сокращенно коды БЧХ), позволяют обнаруживать и
исправлять любое число ошибок. Заданными при кодировании является число ошибок s, которое следует исправить, и общее
число символов, посылаемых в линию, т.е. длина слов n. Числа информационных символов k и контрольных символов m, а также состав контрольных символов подлежат определению.
Коды БЧХ для обнаружения ошибок. Их строят следующим
образом. Если необходимо образовать код с обнаружением четного числа ошибок, то
по заданному числу r находят значения d и s. Дальнейшее кодирование выполняют, как
и ранее. Если требуются обнаружить нечетное число ошибок, то находят ближайшее
меньшее целое число s и кодирование производят так же, как и в предыдущем случае: образующий многочлен дополнительно
умножают на двучлен ![]() . Например, требуются
построить код обнаруживающий семь ошибок при n=15. Находим, что d=8, а ближайшее меньшее значение s=3. Далее определяем многочлен
. Например, требуются
построить код обнаруживающий семь ошибок при n=15. Находим, что d=8, а ближайшее меньшее значение s=3. Далее определяем многочлен ![]() , как
указано в примере 3.5, и умножаем его на двучлен
, как
указано в примере 3.5, и умножаем его на двучлен ![]() , т.е. получаем
, т.е. получаем ![]() . Таким
образом построен код БЧХ(15,4).
. Таким
образом построен код БЧХ(15,4).
11 Лекция №11. Помехоустойчивые коды и методы декодирования корректирующих кодов
Цель лекции: изучение помехоустойчивых кодов и методов декодирования корректирующих кодов
Содержание:
а) коды Рида- Соломона;
б) сверточные коды;
в) классификация корректирующих кодов;
г) методы декодирования корректирующих кодов.
11.1 Коды Рида- Соломона
Коды Рида-Соломона (Reed-Solomon code, R-S code) — это недвоичные циклические коды, символы которых представляют собой m-битовые последовательности, где т — положительное целое число, большее 2. Код (n,к) определен на m-битовых символах при всех n и k, для которых
![]() (11.1)
(11.1)
где k - число информационных битов, подлежащих кодированию, а n - число кодовых символов в кодируемом блоке. Для большинства сверточных кодов Рида-Соломона (n, к)
![]() (11.2)
(11.2)
где t - количество ошибочных битов в символе, которые может исправить код, а n-k = 2t- число контрольных символов. Расширенный код Рида-Соломона можно получить при n = 2m или n= 2m+ 1, но не более того.
Код Рида-Соломона обладает наибольшим минимальным расстоянием, возможным для линейного кода с одинаковой длиной входных и выходных блоков кодера. Для недвоичных кодов расстояние между двумя кодовыми словами определяется (по аналогии с расстоянием Хэмминга) как число символов, которыми отличаются последовательности. Для кодов Рила-Соломона минимальное расстояние определяется следующим образом.
![]() (11.3)
(11.3)
Сверточные коды. Особенностью линейного блочного кода, который описывается двумя целыми числами, n и k, и полиномиальным или матричным генератором является то, что каждый из n-кортежей кодовых слов однозначно определяется k-кортeжeм входного сообщения. Целое число к указывает на число бит данных, которые образуют вход блочного кодера. Целое число п - это суммарное количество разрядов в соответствующем кодовом слове на выходе кодера. Отношение k/n, называемое степенью кодирования кода (code rate), является мерой добавленной избыточности. Сверточный код описывается тремя целыми числами n, k и К, где отношение k/n имеет такое же значение степени кодирования (информация, приходящаяся на закодированный бит), как и для блочного кода; однако п не определяет длину блока или кодового слова, как это было в блочных кодах. Целое число К является параметром, называемым длиной кодового ограничения (constrain! length); оно указывает число разрядов k-кортежа в кодирующем регистре сдвига. Важная особенность сверточных кодов, в отличие от блочных, состоит в том, что кодер имеет память - n-кортежи, получаемые при сверточном кодировании, являются функцией не только одного входного k-кортежа, но и предыдущих К-1 входных k-кортежей. На практике nи к - это небольшие целые числа, а К изменяется с целью контроля мощности и сложности кода.
Методы декодирования корректирующих кодов. Существует несколько вариантов декодирования циклических кодов. Один из них заключается в следующем:
1. Числение остатка (синдрома). Принятую комбинацию делят на образующий многочлен Р(Х). Остаток R(X)=0 означает, что комбинации принята без ошибок;
2. Подсчет веса остатка W. Если вес остатка равен или меньше числа исправляемых ошибок, т.е. W≤s, то принятую комбинацию складывают по модулю 2 с остатком и получают исправленную комбинацию;
3. Циклический сдвиг на один символ влево. Если W>s, то производят циклический сдвиг влево и полученную комбинацию снова делят на образующий многочлен. Если вес остатка W≤s , то циклически сдвинутую комбинацию складывают с остатком и затем циклически сдвигают ее в обратную строну вправо на один символ. В результате получают исправленную комбинацию;
4. Дополнительные циклические сдвиги влево. Если после циклического сдвига на один символ по-прежнему W>s, то производят дополнительные циклические сдвиги влево. При этом после каждого сдвига сдвинутую комбинацию делят на Р(Х) и проверяют вес остатка. При W≤s выполняют действия, указанные в п.3, с той лишь разницей, что обратных циклических сдвигов вправо делают столько, сколько их было сделано влево.
Метод проверки на четность. Если комбинация принята без искажения, то сумма единиц по модулю 2 даст нуль. При искажении какого – либо символа суммирование при проверке может дать единицу. По результату суммирования каждой из проверок составляют двоичное число, указывающее на место искажения.
Мягкое и жесткое декодирование. Для двоичной кодовой системы со степенью кодирования 1/2 демодулятор подает на декодер два кодовых символа за раз. Для жесткого (двухуровневого) декодирования каждую пару принятых кодовых символов можно изобразить на плоскости в виде одного из углов квадрата. Углы помечены двоичными числами (0, 0), (0, 1), (1, 0) и (1, 1), представляющими четыре возможных значения, которые могут принимать два кодовых символа в жесткой схеме принятия решений. Аналогично для 8-уровневого мягкого декодирования каждую пару кодовых символов можно отобразить на плоскости в виде равностороннего прямоугольника размером 8x8, состоящего из 64 точек. В этом случае демодулятор больше не выдает жестких решений; он выдает квантованные сигналы с шумом (мягкая схема принятия решений).
Основное различие между мягким и жестким декодированием по алгоритму Витерби состоит в том, что в мягкой схеме не используется метрика расстояния Хэмминга, поскольку она имеет ограниченное разрешение.
Мажоритарное декодирование. Этот метод заключается в многократной проверке каждого символа принятой кодовой комбинации по специальным таблицам коэффициентов, составленным для каждого варианта (n, k) циклического кода. Значение каждого символа определяется по мажоритарному принципу (слово «мажоритарный» означает большинство), т.е. по принципу голосования. Это означает, что если, например, один из пяти проверок данного символа три показали 1, а две- 0, то символу присваивается значение 1. Если все проверки показали 1 или 0, то символ считается неискаженным и принимается без изменения.
Если при какой-либо проверке окажется равное число 1 и 0, то это означает, что для данного кода произошла неисправимая комбинация ошибок и принятая комбинация должна быть забракована.
Алгоритм Возенкрафта и Фано. Ранее, до того как Витерби открыл оптимальный алгоритм декодирования сверточных кодов, существовали и другие алгоритмы. Самым первым был алгоритм последовательного декодирования, предложенный Уозенкрафтом (Wozencraft) и модифицированный Фано (Fano). В ходе работы последовательного декодера генерируется гипотеза о переданной последовательности кодовых слов и рассчитывается метрика между этой гипотезой и принятым сигналом. Эта процедура продолжается до тех пор, пока метрика показывает, что выбор гипотезы правдоподобен, в противном случае гипотеза последовательно заменяется, пока не будет найдена наиболее правдоподобная. Поиск при этом происходит методом проб и ошибок. Для мягкого или жесткого декодирования можно разработать последовательный декодер, но обычно мягкого декодирования стараются избегать из-за сложных расчетов и большой требовательности к памяти.
Решетчатое (треллис) кодирование. При использовании в системах связи реального времени кодов коррекции ошибок достоверность передачи улучшается за счет расширения полосы частот. Как для блочных, так и для сверточных кодов преобразование каждого k-кортежа входных данных в более длинный n-кортеж кодового слова требует дополнительного расширения полосы пропускания. Вследствие этого в прошлом кодирование не было особенно популярно в узкополосных каналах (таких, как телефонные), в которых расширять полосу частот сигнала было нецелесообразно. Однако приблизительно с 1984 года возникает активный интерес к схемам, где модуляция объединяется с кодированием; такие схемы называются решетчатым кодированием (trellis-coded modulation — ТСМ). Эти схемы позволяют повысить достоверность передачи, не расширяя при этом полосу частот сигнала.
Алгоритм декодирования Витерби. Алгоритм декодирования Витерби был открыт и проанализирован Витерби (Viterbi) в 1967 году. В алгоритме Витерби, по сути, реализуется декодирование, основанное на принципе максимального правдоподобия; однако в нем уменьшается вычислительная нагрузка за счет использования особенностей структуры конкретной решетки кода. Преимущество декодирования Витерби, по сравнению с декодированием по методу "грубой силы", заключается в том, что сложность декодера Витерби не является функцией количества символов в последовательности кодовых слов. Алгоритм включает в себя вычисление меры подобия (или расстояния), между сигналом, полученным в момент времени t1 и всеми путями решетки, входящими в каждое состояние в момент времени t1. В алгоритме Витерби не рассматриваются те пути решетки, которые, согласно принципу максимального правдоподобия, заведомо не могут быть оптимальными. Если в одно и то же состояние входят два пути, выбирается тот, который имеет лучшую метрику; такой путь называется выживающим. Отбор выживающих путей выполняется для каждого состояния. Таким образом, декодер углубляется в решетку, принимая решения путем исключения менее вероятных путей. Предварительный отказ от маловероятных путей упрощает процесс декодирования.
Смысл декодирования Витерби заключается в следующем: если любые два пути сливаются в одном состоянии, то при поиске оптимального пути один из них всегда можно исключить.
Техническая реализация кодирующих и декодирующих устройств. Оценка сложности построения устройств кодирования. Как следует из принципов построения линейных блочных кодов, основными операциями, выполняемыми при кодировании и декодировании, являются суммирование по модулю 2, операции сдвига, запись, считывание и хранение двоичных разрядов. Эти операции могут быть реализованы на стандартных логических элементах. Поэтому сложность схем кодирования и декодирования можно оценить числом таких элементов (например, триггеров).
Рассмотрим принцип построения кодера кода Хемминга. Кодирование сводится к нахождению проверочных разрядов путем сложения по модулю 2 соответствующих информационных элементов. Поскольку на вход кодера символы поступают со скоростью k элементов в единицу времени, а на выходе формируется поток со скоростью n элементов в единицу времени, то для согласования скоростей необходимо буферное устройство памяти, содержащее k ячеек. Информация в буферную память записывается в последовательном коде и на (k+1)-м такте в параллельном коде поступает в кодирующее устройство. Сформированная n-разрядная комбинация в параллельном коде записывается в буферный регистр, откуда с нужной скоростью поступает в канал связи. Поскольку скорость работы кодирующего устройства может быть значительно выше, чем скорость поступления входной информации, то кодер всегда работает в реальном масштабе времени передачи информации.
12 Лекция №12. Системы связи с обратной связью
Цель лекции: изучение характеристик систем с обратной связью и рассмотрение структурной схемы с ОС.
Содержание:
а) характеристики систем с обратной связью и их особенности;
б) структурная схема системы с информационной обратной связью (ИОС) и решающей обратной связью (РОС), характеристики и алгоритмы работы.
12.1 Характеристики систем с обратной связью и их особенности
В системах с ОС ввод в передаваемую информацию избыточности производится с учетом состояния дискретного канала. С ухудшением состояния канала вводимая избыточность увеличивается, и, наоборот, по мере улучшения состояния канала она уменьшается.
В зависимости от назначения ОС различают системы: с решающей обратной связью (РОС), информационной обратной связью (ИОС) и с комбинированной обратной связью (КОС).
Передача с РОС аналогична телефонному разговору в условиях плохой слышимости, когда один из собеседников, плохо расслышав какое-либо слово или фразу, просит другого повторить их еще раз, а при хорошей слышимости или подтверждает факт получения информации, или, во всяком случае, не просит повторения.
Полученная по каналу ОС информация (квитанция) анализируется передатчиком, и по результатам анализа передатчик принимает решение о передаче следующей кодовой комбинации или о повторении ранее переданных. После этого передатчик передает служебные сигналы о принятом решении, а затем соответствующие кодовые комбинации. В соответствии с полученными от передатчика служебными сигналами приемник ПКпр или выдает накопленную кодовую комбинацию получателю информации, или стирает ее и запоминает вновь переданную. В системах с укороченной ИОС, естественно, меньше загрузка обратного канала, но больше вероятность появления ошибок по сравнению с полной ИОС.
В системах с КОС решение о выдаче кодовой комбинации получателю информации или о повторной передаче может приниматься и в приемнике, и в передатчике системы ПДС, а канал ОС используется для передачи как квитанций, так и решений. Системы с ОС подразделяют также на системы с ограниченным числом повторений и с неограниченным числом повторений. В системах с ограниченным числом повторений каждая кодовая комбинация может повториться не более l раз, и в системах с неограниченным числом повторений передача комбинаций повторяется до тех пор, пока приемник или передатчик не примет решение о выдаче этой комбинации потребителю. При ограниченном числе повторений вероятность выдачи получателю неправильной комбинации больше, но зато меньше потери времени на передачу и проще реализация аппаратуры. Заметим, что в системах с ОС время передачи сообщения не остается постоянным и зависит от состояния канала.
Системы с ОС могут отбрасывать либо использовать информацию, содержащуюся в забракованных кодовых комбинациях, с целью принятия более правильного решения. Системы первого типа получили название систем без памяти, а второго — систем с памятью.
Обратной связью могут быть охвачены различные части системы (рисунок 12.1):
1) канал связи, при этом по каналу ОС передаются сведения о принимаемом сигнале до принятия какого-либо решения;
2) дискретный канал, при этом по каналу ОС передаются решения, принятые первой решающей схемой PC1 на основе анализа единичных элементов сигнала;
3) канал передачи данных, при этом по каналу ОС передаются решения, принятые второй решающей схемой РС2 на основе анализа кодовых комбинаций.

Рисунок 12.1 - Обратная связь в системе ПДС
В системах с ИОС также возможны потери верности за счет ошибок в каналах ОС. В укороченных ИОС такие ошибки возникают по причинам, аналогичным вышеизложенным, когда квитанция, соответствующая искаженному сигналу в канале ОС, трансформируется в квитанцию, соответствующую неискаженному сигналу. В результате передатчик не в состоянии обнаружить факт ошибочного приема. В полных ИОС в канале ОС возможны искажения, полностью компенсирующие искажения в прямом канале, в результате чего ошибки не могут быть обнаружены. Поэтому вопросам образования каналов ОС в системах ПДС уделяется очень большое внимание. Каналы ОС обычно образуются в каналах обратного направления связи с помощью методов частотного или временного разделения от каналов передачи полезной информации. Методы ЧРК используют обычно в системах со сравнительно небольшой удельной скоростью передачи, например, при передаче данных со скоростью 600... 1200 бит/с по каналам ТЧ. Во многих системах с РОС применяется структурный метод разделения, когда для сигнала переспроса используется специальная кодовая комбинация, а любая разрешенная кодовая комбинация в приемнике дешифруется как сигнал подтверждения и любая неразрешенная комбинация - как сигнал переспроса. Для защиты от искаженных сигналов, передаваемых по каналам ОС, применяют те же способы, что и для повышения верности полезной информации: корректирующие коды, многократную и параллельную передачи.
12.2 Структурная схема системы с информационной обратной связью (ИОС) и решающей обратной связью (РОС), характеристики и алгоритмы работы
В системах с ИОС (рисунок 12.2,б) по обратному каналу передаются сведения о поступающих на приемник кодовых комбинациях (или элементах комбинации) до их окончательной обработки и принятия заключительных решений. При разговоре по телефону часто используют ретрансляционную ИОС, когда в условиях сильных помех просят собеседника повторить переданное сообщение, чтобы убедиться, что он его воспринял правильно. При правильном повторении передающий дает подтверждение, а при неправильном - повторяет сообщение еще раз. Частным случаем ИОС является полная ретрансляция поступающих на приемную сторону кодовых комбинаций или их элементов. Соответствующие системы получили название ретрансляционных. В более общем случае приемник вырабатывает специальные сигналы, имеющие меньший объем, чем полезная информация, но характеризующие качество ее приема, которые по каналу ОС направляются передатчику. Если количество информации, передаваемое по каналу ОС (квитанции), равно количеству информации в сообщении, передаваемом по прямому каналу, то ИОС называется полной. Если же содержащаяся в квитанции информация отражает лишь некоторые признаки сообщения, то ИОС называется укороченной. Таким образом, по каналу ОС передается или вся полезная информация или информация о ее отличительных признаках, поэтому такая ОС называется информационной.
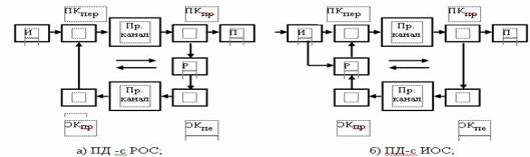
Рисунок 12.2 - Структурные схемы ПД с ОС
ПКпер-передатчик прямого канала; ПКпр- приемник прямого канала;
ОКпер- передатчик обратного канала; ОКпр- приемник обратного канала;
РУ-решающее устойство.
В системах с РОС (рисунок 12.2, а) приемник, приняв кодовую комбинацию и проанализировав ее на наличие ошибок, принимает окончательное решение о выдаче комбинации потребителю информации или о ее стирании и посылке по обратному каналу сигнала о повторной передаче этой кодовой комбинации (переспрос). Поэтому системы с РОС часто называют системами с переспросом, или системами с автоматическим запросом ошибок (АЗО). В случае принятия кодовой комбинации без ошибок приемник формирует и направляет в канал ОС сигнал подтверждения, получив который, передатчик ПКпер передает следующую кодовую комбинацию. Таким образом, в системах с РОС активная роль принадлежит приемнику, а по обратному каналу передаются вырабатываемые им сигналы решения (отсюда и название —решающая ОС).
В системе с РОС по прямому каналу передаются информационные комбинации длиной п единичных элементов и команды решения, а по каналу обратной связи — служебные комбинации. В системе с ИОС по прямому каналу передаются информационные комбинации длиной k единичных элементов и команды решения, а по каналу ОС — проверочные комбинации длиной n—k единичных элементов. При n—k<k система с РОС подобна системе с укороченной ОС, при n—k=k — системе ИОС с полной ОС. Нередко при сравнении систем с РОС и ИОС игнорируется это обстоятельство и сопоставляются системы с РОС при n—k≤k с системой с полной (ретрансляционной) ОС. В результате сравнения несопоставимых систем делается вывод о том, что скорость передачи в системе с РОС указанного типа вдвое выше, чем в рассмотренной системе с ИОС.
Виды системы с РОС: системы с ожиданием служебных сигналов, системы с непрерывной передачей и блокировкой, системы с адресным переспросом. В настоящее время известны многочисленные алгоритмы работы систем с ОС. Наиболее распространенными среди них являются системы: с РОС с ожиданием сигнала ОС; с безадресным повторением и блокировкой приемника и с адресным повторением.
Системы с ожиданием после передачи кодовой комбинации либо ожидают сигнал обратной связи, либо передают ту же кодовую комбинацию, 'но передачу следующей кодовой комбинации начинают только после получения подтверждения по ранее переданной комбинации.
Системы с блокировкой осуществляют передачу непрерывной последовательности кодовых комбинаций при отсутствии сигналов ОС по предшествующим S комбинациям. После обнаружения ошибок в (S+1)-й комбинации выход системы блокируется на время приема S комбинаций, в запоминающем устройстве приемника системы ПДС стираются S ранее принятых комбинаций, и посылается сигнал переспроса. Передатчик повторяет передачу S последних переданных кодовых комбинаций.
Системы с адресным повторением отличает то, что кодовые комбинации с ошибками отмечаются условными номерами, в соответствии с которыми передатчик производит повторную передачу только этих комбинаций.
Алгоритм защиты от наложения и потери информации. Системы с ОС могут отбрасывать либо использовать информацию, содержащуюся в забракованных кодовых комбинациях, с целью принятия более правильного решения. Системы первого типа получили название систем без памяти, а второго - систем с памятью.
13 Лекция №13. Сжатие данных в ЦСС
Цель лекции: изучение алгоритмов сжатия данных и видов сжатия данных.
Содержание:
а) алгоритмы сжатия без потерь;
б) сжатие аудиосигналов;
в) сжатие изображения.
13.1 Алгоритмы сжатия без потерь
Код Хаффмана. Код Хаффмана (Huffman code) (201 - это свободный от префикса код, который может давать самую короткую среднюю длину кода я для данного входного алфавита. Самая короткая средняя длина кода для конкретного алфавита может быть значительно больше энтропии алфавита источника, и тогда эта невозможность выполнения обещанного сжатия данных будет связана с алфавитом, а не с методом кодирования. Часть алфавита может быть модифицирована для получения кода расширения, и тот же метод повторно применяется для достижения лучшего сжатия. Эффективность сжатия определяется коэффициентом сжатия. Эта мера равна отношению среднего числа бит на выборку до сжатия к среднему числу бит на выборку после сжатия.
Код Лемпеля-Зива –Уэлча. Основной сложностью при использовании кода Хаффмана является то, что вероятности символов должны быть известны или оценены и как кодер, так и декодер должны знать дерево кодирования. Если дерево строится из необычного для кодера алфавита, канал, связывающий кодер и декодер, должен также отправлять кодирующее дерево как заголовок сжатого файла. Эти служебные издержки уменьшат эффективность сжатия, реализованную с помощью построения и применения дерева к алфавиту источника. Алгоритм Лемпеля-Зива (Lempel-Ziv) и его многочисленные разновидности используют текст сам по себе для итеративного построения синтаксически выделенной последовательности кодовых слов переменной длины, которые образуют кодовый словарь.
Алгоритм Хаффмана в факсимильной связи.
Факсимильная передача — это процесс передачи двухмерного образа как последовательности последовательных строчных разверток. В действительности наиболее распространенными образами являются документы, содержащие текст и цифры. Положение строчной развертки и положение вдоль развертки квантуются в пространственные расположения, которые определяют двухмерную координатную сетку элементов картинки, называемых пикселями. Ширина стандартного документа МККТТ определяется равной 8,27 дюймов (20,7 см ), а длина- 11,7 дюймов (29,2 см), почти 8,5 дюймов на 11,0 дюймов. Пространственное квантование для нормального разрешения составляет 1728 пикселей/строку и 1188 строк/документ. Стандарт также определяет квантование с высоким разрешением с теми же 1728 пикселями/строку, но с 2376 строками/документ. Общее число отдельных пикселей для факсимильной передачи с нормальным разрешением составляет 2 052 864, и оно удваивается для высокого разрешения. Для сравнения, число пикселей в стандарте NTSC (National Television Standards Committee — Национальный комитет по телевизионным стандартам) коммерческого телевидения составляет 480 х 460, или 307 200. Таким образом, факсимильное изображение имеет разрешение в 6,7 или 13,4 раза больше разрешения стандартного телевизионнго образа.
Сжатие аудиосигналов.
Аудиосжатие широко применяется в потребительских и профессиональных цифр< аудиопродуктах, таких как компакт-диски (compact disc — CD), цифровая аудиолента (digital audio type — DAT), мини-диск (mini-disk — MD), цифровая компакт-кассета (digital compact cassette — DCC), универсальный цифровой диск (digital versatile disc. DVD), цифровое аудиовещание (digital audio broadcasting — DAB) и аудиопродукция формате МРЗ от экспертной группы по вопросам движущегося изображения (М< Picture Experts Group — (MPEG). К тому же сжатие речи в телефонии, в частности, сотовой телефонии, требуемое для экономии полосы частот и сбережения времени, ни батареи, дало начало процессу разработки множества стандартов сжатия речи, личные алгоритмы применимы к речевым и потребительским сигналам более широкой полосы частот. Аудио- и речевые схемы сжатия можно для удобства разделить согласно приложениям, что отражает некоторую меру приемлемого качества.
Адаптивная дифференциальная ИКМ (АДИКМ). Используя прошлые данные для измерения (т.е. квантования) новых переходим от обычной импульсно-кодовой модуляции (pulse-code modulation — PCM) к дифференциальной (differential PCM — DPCM). В DPCM предсказание следующего выборочного значения формируется на основании предыдущих значений. Устройства квантования называются мгновенными устройствами квантования или устройствами квантования без памяти, так как цифровые преобразования основаны на единичной (текущей) входной выборке. Этими свойствами были неравновероятные уровни источника и зависимые выборочные значения. Корреляционные характеристики источника можно представить во временной области с помощью выборки его автокорреляционной функции и в частотной области — его спектром мощности. Если изучается спектр мощности Gx(f) кратковременного речевого сигнала, как изображено на рисунке 9.2, то видим, что спектр имеет глобальный максимум в окрестности от 300 до 800 Гц и убывает со скоростью от 6 до 12 дБ/октаву. Эта операция производится в контуре сказания и сравнения, верхний контур кодера изображен на рисунке 13.2. Кодер корректирует свои предсказания, составляя сумму предсказанного значения и ошибки предсказания.
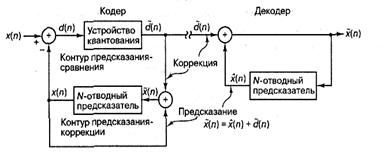
Рисунок 13.1 - N- отводный дифференциальный импульсно-кодовый модулятор с предсказанием
Эта модель, использующая 12-отводный синтезатор речи, нашла применение в детских говорящих играх.
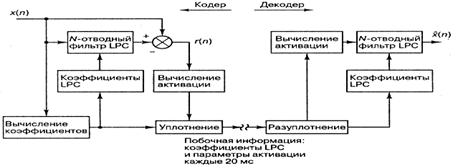
Рисунок 13.2 - Блочная диаграмма: моделирование речи с помощью линейного кодера с предсказанием
Алгоритм сжатия MPEG, уровни 1,2,3.
Международная организация по стандартизации (International Organization for Standardization - ISO) и экспертная группа по вопросам движущегося изображения (Motion Picture Experts Group - MPEG) разработали стандарт аудиосжатия для сигнала, синхронизированного с сжатым видеосигналом, известный как MPEG. В этой схеме объединены свойства MUS1CAM (Masking pattern adaptive Universal Subband Integrated Coding And Multiplexing - универсальные интегральные средства кодирования и уплотнения по поддиапазонам с маскировкой и адаптацией к кодограмме) и ASPEC (Adaptive Spectral Perceptual Entropy Coding — адаптивное спектрально-восприимчивое кодирование энтропии). В схеме использованы три уровня (коды) увеличивающейся сложности и улучшающейся субъективной производительности. Входные частоты дискретизации равны 32, 44,1 и 48 кГц, а биты на выход подаются со скоростью от 32 до 192 Кбит/с (монофонический канал) или со скоростью от 64 до 384 Кбит/с (стереофонический канал). Стандарт поддерживает режим работы единственного канала, стереорежим, двойственный режим работы канала (для двуязычных аудиопрограмм) и дополнительный совместный стереорежим. В последнем режиме два кодера для левого и правого каналов могут поддерживать друг друга, используя общие статистики с целью снижения скорости передачи бит аудиосигнала, даже большего, чем это возможно при монофонической передаче.
На рисунке 13.3 представлена блочная диаграмма аудиокодера и декодера уровней I и II стандарта MPEG.
На уровне III стандарта MPEG/ISO (MP3) достигается разрешение более высокой частоты, которое весьма точно соответствует критической разрешающей способности человека.
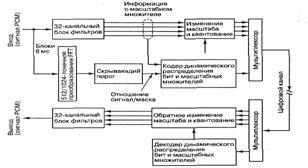
Рисунок 13.3 - Блочная диаграмма аудиокодера и декодера, уровни I и II
Сжатие изображения
Мы часто слышали старое высказывание: Картина стоит тысячи слов. Верно ли оно? 1000 слов содержит 6000 знаков, которые, будучи закодированы как 7-битовые символы ASCII, требуют в общей сложности 42 000 бит. Какого размера образ (или картина) может быть описан с помощью 42 000 бит?
Существует множество стандартов, которые были разработаны для сжатия изображений.
Алгоритм сжатия JPEG. JPEG (Joint Photography Experts Group - объединенная группа экспертов в области фотографии) - это общее название, которое дано стандарту ISO/JPEG 10918-1 и стандарту ITU-T Recommendation T.81 "Цифровое сжатие, постоянных изображений непрерывного тона", JPEG, в основном, известен как основанная на преобразовании схема сжатия с потерями.
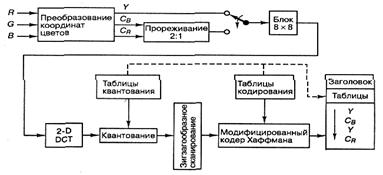
Рисунок 13.4 - Блочная диаграмма кодера JPEG
Применение вейвлет – преобразования для сжатия изображений.
Рекурсивный (волновой) алгоритм. Английское название рекурсивного сжатия — wavelet. На русский язык оно также переводится как волновое сжатие и как сжатие с использованием всплесков. Этот вид архивации известен довольно давно и напрямую исходит из идеи использования когерентности областей.
Заключение
В заключение рассмотрим таблицы, в которых сводятся воедино параметры различных алгоритмов сжатия изображений, рассмотренных нами выше.
|
|
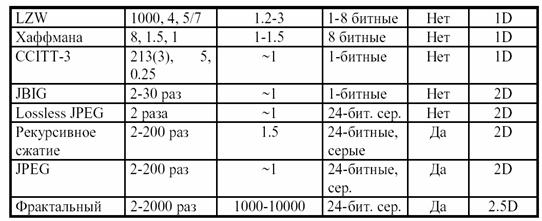
Список литературы
1. Скляр Б. Цифровая связь. Теоретические основы и практическое применение: 2-е изд. /Пер. с англ. М.: Издательский дом «Вильямс», 2003. 1104 с.
2. Прокис Дж. Цифровая связь. Радио и связь, 2000.-797с.
3. А.Б. Сергиенко. Цифровая обработка сигналов: Учебник для вузов. - М.:-2002.
4. Шварцман В.О., Емельянов Г.А. Теория передачи дискретной информации. – М.: Связь, 1979. -424 с.
5. Передача дискретных сообщений / Под ред. В. П. Шувалова. - М.: Радио и связь, 1990. -464 с.
6. Емельянов Г. А., Шварцман В. О. Передача дискретной информации. - М.: Радио и связь, 1982. - 240 с.
7. Дмитриев В.И. Прикладная теория информации: Учебник. – М.: Высш.шк., 1989.
8. Тутевич В.Н. Телемеханика: Учебное пособие.- М.: Высш. Шк., 1985. -423 с.
9. Ватолин Д.С. Алгоритмы сжатия изображений. Методическое пособие. Издательский отдел факультета Вычислительной Математики и Кибернетики МГУ им. М.В.Ломоносова (лицензия ЛР № 040777 от 23.07.96), 1999 г. — 76 с.