 Научные и курсовые работы |
Главная
Исторические личности
Военная кафедра
Ботаника и сельское хозяйство
Бухгалтерский учет и аудит
Валютные отношения
Ветеринария
География
Геодезия
Геология
Геополитика
Государство и право
Гражданское право и процесс
Естествознанию
Журналистика
Зарубежная литература
Зоология
Инвестиции
Информатика
История техники
Кибернетика
Коммуникация и связь
Косметология
Кредитование
Криминалистика
Криминология
Кулинария
Культурология
Логика
Логистика
Маркетинг
Наука и техника Карта сайта
Контрольная работа: Измерение напряжения
Контрольная работа: Измерение напряжения
Задача 1.
С помощью селективного микровольтметра проводились многократные измерения в одинаковых условиях ЭДС, возникающей в антенне микровольтметра. Считая, что случайные погрешности имеют нормальный закон распределения, определить на основании заданного количества измерений:
1) действительное значение (среднее арифметическое ![]() ) измеряемой ЭДС;
) измеряемой ЭДС;
2) среднеквадратическое отклонение погрешности измерения ![]() ;
;
3) максимальную погрешность, принятую для нормального закона
распределения, ![]() ;
;
4) наличие грубых погрешностей (промахов) в результатах измерения;
5) среднеквадратическое отклонение результата измерения (среднего
арифметического значения) ![]() ;
;
6) доверительный интервал для результата измерения при доверительной
вероятности ![]() ;
;
7) имеется ли систематическая составляющая в погрешности измерения ЭДС, в качестве истинного значения принять расчетное значение ЭДС Ер
Исходные данные:
| № измерения | E, мкВ |
| 1 | 24,3 |
| 2 | 24,9 |
| 3 | 24,66 |
| 4 | 25,74 |
| 5 | 27,82 |
| 14 | 25,64 |
| 15 | 28,5 |
| 16 | 25,5 |
| 17 | 28,0 |
Доверительная вероятность Рд = 0,95
Расчетное значение ЭДС Ер=24,28 мкВ
Решение:
9 наблюдений 1-5 и 14-17
Представим промежуточные расчеты в виде таблицы:
| № п/п | № измерения |
Ei, мкВ |
Ei - |
(Ei - |
| 1 | 1 | 24,3 | -1,81778 | 3,30432 |
| 2 | 2 | 24,9 | -1,21778 | 1,48298 |
| 3 | 3 | 24,66 | -1,45778 | 2,12512 |
| 4 | 4 | 25,74 | -0,37778 | 0,14272 |
| 5 | 5 | 27,82 | 1,70222 | 2,89756 |
| 6 | 14 | 25,64 | -0,47778 | 0,22827 |
| 7 | 15 | 28,5 | 2,38222 | 5,67498 |
| 8 | 16 | 25,5 | -0,61778 | 0,38165 |
| 9 | 17 | 28,0 | 1,88222 | 3,54276 |
| ∑ | 235,06 | 0,00000 | 19,78036 |
1) Среднее значение ЭДС:
![]() мкВ
мкВ
2) Среднеквадратическое отклонение ![]() погрешности
случайной величины E:
погрешности
случайной величины E:
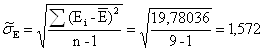 мкВ
мкВ
3) Максимальная погрешность, принятая для нормального закона распределения,
![]() определяется по правилу 3
сигм:
определяется по правилу 3
сигм:
![]() мкВ
мкВ
4) Грубые погрешности (промахи): Грубыми погрешностями по критерию
трех сигм считаем те измерения, которые отличаются от действительного значения ![]() на величину, большую
на величину, большую ![]()
Нет измерений, для которых ![]() мкВ
мкВ
Следовательно, грубых промахов нет - ни одно измерение не исключается
5) среднеквадратическое отклонение результата измерения ![]() ;
;
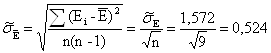 мкВ
мкВ
6) доверительный интервал для результата измерения ЭДС при
доверительной вероятности ![]() = 0,95
находим из условия, что E имеет распределение Стьюдента.
= 0,95
находим из условия, что E имеет распределение Стьюдента.
По таблице значений коэффициента Стьюдента находим значение:
![]()
Доверительный интервал рассчитывается по формуле:
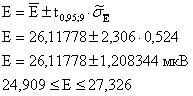
7) Систематическая составляющая погрешности измерения ЭДС:
![]() мкВ
мкВ
погрешность измерения напряжение частота
Задача 2.
На выходе исследуемого устройства имеет место периодическое напряжение, форма которого показана на рис. 1. Это напряжение измерялось пиковым вольтметром (ПВ), а также вольтметрами средневыпрямленного (СВ) и среднеквадратического (СК) значений, проградуированных в среднеквадратических значениях синусоидального напряжения. Каждый из вольтметров имеет как открытый, так и закрытый вход.
Требуется определить:
1) среднее Ucp, средневыпрямленное Ucp.В и среднеквадратическое Ucp значения выходного напряжения заданной формы;
2) коэффициенты амплитуды КА и формы Кф выходного напряжения;
3) напряжения, которые должны показать каждый их трех указанных вольтметров с открытым (ОТКР) или закрытым (ЗАКР) входом;
4) оценить относительную погрешность измерения всех вычисленных согласно п. 3 напряжений, если используемые измерительные приборы имеют класс точности δпр и предельные значения шкалы UПР.
| Исходные данные | E, мкВ |
|
UПР, В |
15 |
|
UМ, В |
10 |
| СВ | ЗАКР |
| СК | ОТКР |
| Рисунок | ж |
| ПВ | ОТКР |
|
δпр, % |
2,5 |
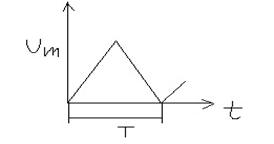
рис.1
m = 0
n = 4
![]() мс
мс
Решение:
1) Рассчитываем среднее значение напряжения:
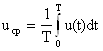
Определенный интеграл численно равен площади под треугольной
функцией ![]() на интервале
интегрирования:
на интервале
интегрирования:
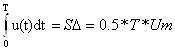
Следовательно,
![]()
Cредневыпрямленное значение напряжения:
![]()
Среднеквадратическое значение напряжения:
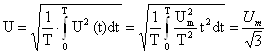
2) Определяем коэффициенты формы и амплитуды напряжения:
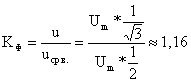
![]()
3) рассчитываем градуировочные коэффициенты каждого вольтметра:
Пикового напряжения:
![]()
![]()
Средневыпрямленного напряжения:
![]()
|
|
Квадратичного напряжения:
![]()
![]()
При открытом входе вольтметр будет измерять весь сигнал:
![]()
При закрытом входе вольтметр будет измерять сигнал с вычетом постоянной составляющей, равной среднему значению:
![]()
![]() = 10
В
= 10
В
![]()
Вольтметр пикового напряжения. Вход открытый
![]() В
В
Вольтметр средневыпрямленного напряжения. Вход закрытый
![]() В
В
Вольтметр квадратичного напряжения. Вход открытый
![]() В
В
4) Оцениваем относительную погрешность измерения
Вольтметр пикового напряжения:
![]() %
%
Вольтметр средневыпрямленного напряжения:
![]() %
%
Вольтметр квадратичного напряжения:
![]() %
%
Задача 3.
В лаборатории имеется цифровой частотомер со следующими параметрами: частота опорного кварцевого генератора 1 МГц + δ0, значение коэффициента деления частоты, определяющее время счета импульсов, можно изменять в пределах от 103 до 107 ступенями, кратными 10. Требуется:
1. Построить в логарифмическом масштабе по f график зависимости абсолютной погрешности измерения частоты fx в диапазоне от f мин до fмакс при заданном коэффициенте деления пд.
2. Выбрать допустимое значение коэффициента деления частоты и определить соответствующее ему время счета для измерения частоты f1, с суммарной погрешностью, не превышающей значения δfдоп.
Исходные данные |
|
|
f мин , Гц |
5 |
|
δfдоп, % |
3,5*10-1 |
|
f1 , мГц |
0,5 |
|
f макс , мГц |
25 |
|
пд |
107 |
|
δ0 |
4*10-6 |
Решение:
1. Относительная погрешность измерения определяется по формуле:
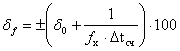
Время счета импульсов определяется по формуле:
![]() ,
,
где f0 – частота опорного кварцевого генератора (1 МГц)
![]() с
с
Отсюда относительная погрешность измерения:
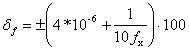
Абсолютная погрешность измерения определяется по формуле:
![]()
Сводим промежуточные расчеты в таблицу:
|
Частота fx |
Относительная погрешность δf |
Абсолютная погрешность ∆f, Гц |
| 5 Гц | 2,00040000 | 0,1000200 |
| 10 Гц | 1,00040000 | 0,1000400 |
|
100 Гц (102) |
0,10040000 | 0,1004000 |
|
1 кГц (103) |
0,01040000 | 0,1040000 |
|
10 кГц (104) |
0,00140000 | 0,1400000 |
|
100 кГц (105) |
0,00050000 | 0,5000000 |
|
1 МГц (106) |
0,00041000 | 4,1000000 |
|
10 МГц (107) |
0,00040100 | 40,1000000 |
|
25 Мгц (2,5∙107) |
0,00040040 | 100,1000000 |
По результатам расчетов строим график в логарифмическом масштабе:
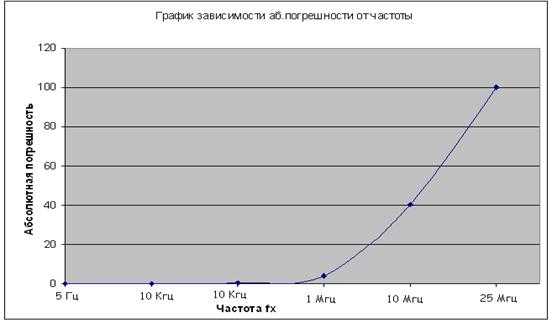
Рисунок 1. График зависимости абсолютной погрешности от частоты
2. Определяем допустимое значение коэффициента деления частоты
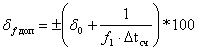
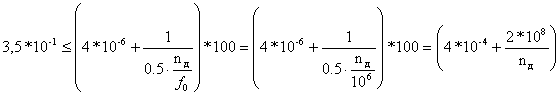
Находим из этого условия границу коэффициента деления частоты:
![]()
Следовательно, необходимый коэффициент деления частоты должен быть равен:
![]()
Время счета:
![]() с
с
Задача 4.
При проектировании оборудования осуществлялись прямые измерения индуктивности катушек L, емкости конденсаторов С, сопротивления резисторов г и R, предназначенных для изготовления параллельных колебательных контуров (рис. 4.1а). В зависимости от варианта требуется определить один из следующих параметров колебательного контура: резонансную частоту f0, добротность Q, сопротивление Zoe, полосу пропускания контура по уровню 0,707 (-3 дБ) 2∆f0,7, а также оценить возможные погрешности этих параметров, обусловленные случайными погрешностями измерения элементов контура.
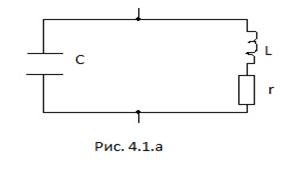
| Рисунок | а |
| Найти | Zoe |
| L, мкГн | 44 |
| C, пФ | 54 |
| r, Ом | 32 |
| R, Ом | - |
|
±δL |
3.2 |
|
±δC |
0.4 |
|
±δr |
1.4 |
|
±δR |
2.5 |
Решение:
1. Требуется определить сопротивление Zoe:
Резонансная частота
![]()
![]()
![]()
Сопротивление
![]()
Погрешность

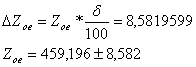
Задача 5.
С помощью осциллографа методом калиброванной шкалы измеряется максимальное значение напряжения в виде последовательности однополярных прямоугольных импульсов. Размах осциллограммы импульса равен h при коэффициенте отклонения, равном KОТК. Определить максимальное значение напряжения, относительную и абсолютную погрешности измерения, если погрешность калибровки шкалы и измерения размаха осциллограммы равны соответственно ±δК (%) и ±∆h (мм). Погрешностью преобразования, обусловленной нелинейностью амплитудной характеристики осциллографа, пренебречь.
Можно ли использовать осциллограф с верхней граничной частотой полосы пропускания fв для исследования данного напряжения, если длительность импульса равна τн, а время нарастания фронта импульса равно τф = aτн?
| h, мм | 54 |
|
δК, % |
4 |
|
τн, мкс |
20 |
|
fв, МГц |
1.5 |
| ∆h, мм | 0.5 |
|
KОТК, В/см |
1 |
|
a |
0.01 |
Решение:
1. Амплитуду сигнала определяем из соотношения:
![]()
kо - коэффициент отклонения, В/дел.,
LА - размер амплитуды, в делениях,
![]() В/см
В/см
Относительная погрешность измерения амплитуды
![]()
dkо - относительная погрешность коэффициента отклонения,
dВА - относительная визуальная погрешность.
![]() см
см
2. Для того, чтобы осциллограф можно было использовать для исследования, полоса пропускания должна удовлетворять соотношению:
![]()
Следовательно, осциллограф использовать нельзя.