рефераты

Научные и курсовые работы


Главная
Исторические личности
Военная кафедра
Ботаника и сельское хозяйство
Бухгалтерский учет и аудит
Валютные отношения
Ветеринария
География
Геодезия
Геология
Геополитика
Государство и право
Гражданское право и процесс
Естествознанию
Журналистика
Зарубежная литература
Зоология
Инвестиции
Информатика
История техники
Кибернетика
Коммуникация и связь
Косметология
Кредитование
Криминалистика
Криминология
Кулинария
Культурология
Логика
Логистика
Маркетинг
Наука и техника Карта сайта

Лабораторная работа: Оценка качества и точности полевых измерений

Лабораторная работа: Оценка качества и точности полевых измерений

Лабораторная работа

Пояснительная записка расчетно-графической работы №: 19 страниц, 5 приложений, таблиц _6_

Цель работы – освоить методику, выполнить оценку качества полевых измерений, уравнительные вычисления в полигонометрических сетях с одной узловой точкой, оценку точности полевых измерений, оценку точности уравненных значений, а также уравнивание полигонометрической строгим способом.


Содержание

1.1 Исходные данные

1.2 Предварительные вычисления. Вычисление рабочих координат

1.3 Уравнивание угловых и линейных величин

1.4 Оценка точности полевых измерений

1.5 Оценка точности уравненных значений координат узловой точки

1.6 Вычисление весов уравненных значений координат узловой точки

1.7 Оценка точности вычисления координат узловой точки

ПРИЛОЖЕНИЕ А

ПРИЛОЖЕНИЕ Б

ПРИЛОЖЕНИЕ В

ПРИЛОЖЕНИЕ Г

ПРИЛОЖЕНИЕ Д


1.1  Исходные данные

Таблица 1 – Исходные данные

T12
Угол град мин сек X Y
T4-T12 51 12 31 37886,284 34831,923
T01
Угол град мин сек X Y
T2-T01 138 27 9 40693,57 36113,38
T18
Угол град мин сек X Y
T19-T18 270 11 58 39186,582 39109,988

Таблица 2 – Ведомость углов (левых) и горизонтальных проложений

Точки Углы (лев) Горизонт
Стояния Визиров Град Мин Сек пролож
T4
T12 171 43 45 441,325
11
T12
11 193 18 52 395,109
10
11
10 187 32 17 312,470
9
10
9 200 53 34 446,753
8
9
8 167 10 8 397,031
7
8
7 158 48 35 308,962
6
7
6 189 45 22
6a
 Точки Углы (лев) Горизонт
Стояния Визиров Град Мин Сек пролож
T19
T18 174 48 30 302,092
17
T18
17 167 37 29 313,561
16
17
16 175 18 8 357,996
15
16
15 185 11 25 527,923
14
15
14 207 12 18 523,302
13
14
13 167 11 42 346,434
6
13
6 330 53 45
6a
 Точки Углы (лев) Горизонт
Стояния Визиров Град Мин Сек пролож
T2
T01 167 43 48 363,080
2
T01
2 214 12 1 442,312
3
2
3 201 10 35 346,536
4
3
4 176 36 11 403,438
5
4
5 149 28 57 456,024
6
5
6 92 46 15
6a

1.2  Предварительные вычисления. Вычисление рабочих координат пунктов

Цель предварительных вычислений в полигонометрии – определение качества полевых измерений и соответствия их по точности требованиям инструкции, а также подготовка результатов измерений для уравнительных вычислений.

В результате предварительных вычислений определяют невязки ходов и полигонов и сравнивают их с предельными значениями, установленными для данного класса или разряда соответствующими инструкциями.

Угловую невязку fβ находят для разомкнутого хода по формуле

Далее распределяем полученную угловую невязку поровну на каждый угол вычисляя поправки по формуле:

.

По исправленным за угловую невязку углам вычисляют дирекционные углы


Далее вычисляют приращения координат и определяют невязки в приращениях по формулам:

По невязкам и  находят абсолютную и относительную линейные невязки хода или полигона

Невязки и  распределяют прямо пропорционально длинам линий хода

 и  

По исправленным за поправки приращениям координат вычисляют координаты пунктов хода.

1.3  Уравнивание угловых и линейных величин

За узловую обычно принимают линию того звена, в котором наибольшее число их, В данном случае за узловое принято направление на вспомогательную точку, не входящую в сеть 6-6а. По каждому звену, начиная от твёрдой линии, вычисляют дирекционные углы узловой линии

где - исходный дирекционный угол

- сумма левых по ходу углов

(n+1) – число углов в звеньях

Значения вычисленных дирекционных углов записывают в таблицу 3. Вычисляют среднее весовое значение дирекционного угла узловой линии по формуле

 

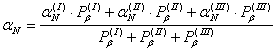
Веса получают по формуле:

где с – постоянное число, выбираемое произвольно, в данном случае с=1.

Полученное значение дирекционного угла узлового направления рассматривают как твёрдое и вычисляют невязки по ходам:

Эти невязки распределяют поровну (с противоположным знаком) на каждый измеренный угол звена и находят первые поправки к углам и вычисляют уравненное значение углов.

Таблица 3 – Вычисление средневесового значения дирекционного угла

№ хода Вес Р Значение дирекционного Средневесовое значение

f β

Pβ*fβ2
1/n+1 угла узловой точки дирекционного угла
1 0,1667 60 24 57 -9 12,041667
2 0,1429 60 25 4 60 25 6 -2 0,3214286
3 0,1429 60 25 17 11 18,565714
Сумма 0,4524 30,9288

По уравненным значениям дирекционных углов вычисляют приращения координат по формулам:

,

где - уравненный дирекционный угол

 - горизонтальное проложение. Затем вычисляют средневесовое значение координат узловой точки по формуле:

Веса вычисляют по формуле:

где с – постоянное число, выбираемое произвольно.

Результаты записаны в таблице 4 для значения координаты Х и в таблице 5 для значения координаты У.


Таблица 4 – Вычисление средневесового значения координаты Х

№ хода Вес Р Вычисленная координата Х Средневесовое значение

f х

Pх*fх2
с/[di] узловой точки координаты Х
1 0,2000 38927,705 -0,010 1,873E-05
2 0,1667 38927,783 38927,715 0,068 0,0007615
3 0,1667 38927,659 -0,056 0,0005223
Сумма 0,5333 0,0013026

Таблица 5 – Вычисление средневесового значения координаты У

№ хода Вес Р Вычисленная координата У Средневесовое значение

f у

Pу*fу2
c/[di] узловой точки координаты У
1 0,2000 36802,446 -0,038 0,000291
2 0,1667 36802,489 36802,484 0,005 4,527E-06
3 0,1667 36802,525 0,041 0,0002743
Сумма 0,5333 0,0005698

1.4  Оценка точности полевых измерений

Качество полевых измерений оценивается по средней квадратической ошибке измерения угла. Средняя квадратическая ошибка единицы веса вычисляется по формуле:

,

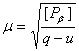где q – число звеньев в сети, u – число узловых точек. Тогда μ=3,9.

Средние квадратические ошибки ошибки μx и μy единицы веса абсцисс и ординат:

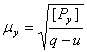
1.5  Оценка точности уравненных значений координат узловой точки

Определяют средние квадратические ошибки уравновешенных координат узловой точки:

 

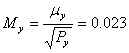
Определяют средние квадратические ошибки уравненного значения дирекционного угла

Рассмотренная оценка точности координат при раздельном уравнивании сети – приближённая, так как она производится не по строгим формулам теории ошибок.


1.6  Вычисление весов и координат узловой точки

Веса вычисляют по формулам:

,

Где

В данных формулах:

μ – коэффициент влияния случайных ошибок линейных измерений (μ= 0.0005)

L – расстояние между начальной и узловой точкой

θ – дирекционный угол замыкающей линии

n – число сторон в ходе

 L1=

 1895,54962

 Мх1=

 0,001923193

 L2=

 2228,83135

 Му1=

 0,000475367

 L3=

 2321,97906

 Мх2=

 0,000749624
θ1= 158,682373

 Му2=

 0,002011049
θ2= 62,1437876

 Мх3=

 0,000805679
θ3= 263,599044

 Му3=

 0,00302386
μ*μ= 0,00000025

 Px1=

 520

 Py1=

 2104

 Px2=

 1334

 Py2=

 497

 Px3=

 1241

 Py3=

 331

Тогда средневесовые значения координат узловой точки равны:

 X0=

 38927,720

 Y0=

 36802,462

1.7  Оценка точности вычисления координат узловой точки

Оценка точности уравненных координат узловой точки выполняется по формулам, приведённым в разделе 1.5. Результаты определения весов узловой точки записывают в таблицу 6.

Таблица 6 – Ведомость вычисления весов узловой точки

№ ходов

f x

 P x

Px fx2

f y

P y

P y fy2

 Примеч
1 0,010 520 0,048693 0,038 2104 3,061263 0,026
2 0,068 1334 6,095149 0,005 497 0,013507 0,017
3 0,056 1241 3,889925 0,041 331 0,544178
Сумма 3095 2932

 Мх=

 0,05 м

 Му=

 0,03 м
 М= 0,06 м

ПРИЛОЖЕНИЕ А

В Е Д О М О С Т Ь
ЛИНИЯ № 1
ВЫЧИСЛЕНИЯ КООРДИНАТ ТОЧЕК ТЕОДОЛИТНОГО ХОДА
Точки Измеренные углы (гор) Дирекционные углы Гор прол Приращения коорд Координаты № точек
Стояния Визиров Град Мин Сек Град Мин Сек Вычисленные
Уравненные
 Х  У  Х  У
Т2
Т01 138 27 9 40693,570 36113,380 Т01
Т2 1 0,008 0,002
Т01 167 43 48 126 10 58 363,080 -214,349 293,056 40479,229 36406,437 2
2 167 43 49 -214,341 293,057
Т01 1 0,010 0,002
2 214 12 1 160 22 60 442,312 -416,640 148,495 40062,599 36554,935 3
3 214 12 2 -416,630 148,498
2 1 0,008 0,002
3 201 10 35 181 33 36 346,536 -346,408 -9,434 39716,199 36545,503 4
4 201 10 36 -346,400 -9,432
3 1 0,009 0,002
4 176 36 11 178 9 48 403,438 -403,231 12,930 39312,977 36558,435 5
5 176 36 12 -403,222 12,932
4 1 0,010 0,002
5 149 28 57 147 38 46 456,024 -385,230 244,040 38927,757 36802,477 6
6 149 28 58 -385,220 244,042
5 0 0,007 0,001
6 263 0 53 230 39 39 308,962 -195,854 -238,953 38731,910 36563,525 7
7 263 0 53 -195,847 -238,952
6 1 0,009 0,002
7 201 11 25 251 51 5 397,031 -123,668 -377,279 38608,250 36186,248 8
8 201 11 26 -123,660 -377,277
7 0 0,010 0,002
8 192 49 52 264 40 57 446,753 -41,403 -444,830 38566,857 35741,419 9
9 192 49 52 -41,393 -444,828
8 1 0,007 0,002
9 159 6 26 243 47 24 312,470 -138,007 -280,342 38428,857 35461,079 10
10 159 6 27 -138,000 -280,341
9 0 0,009 0,002
10 172 27 43 236 15 7 395,109 -219,500 -328,528 38209,366 35132,552 11
11 172 27 43 -219,491 -328,526
10 1 0,010 0,002
11 166 41 8 222 56 16 441,325 -323,092 -300,632 37886,284 34831,923 T12
Т12 166 41 9 -323,082 -300,629 37886,284 34831,923
11 0
T12 188 16 15 231 12 31
T4 188 16 15

[Х ф] [Yф]

 -2807,382 -1281,478
P 4313,040

[Х т] [Y т]

 -2807,286 -1281,457

f β

 -8

f x f y

 -0,096 -0,021

f l

 0,098

f l/P

 0,000023
допуск 0,000100
поправка 0,009

ПРИЛОЖЕНИЕ Б

В Е Д О М О С Т Ь
ЛИНИЯ № 2
ВЫЧИСЛЕНИЯ КООРДИНАТ ТОЧЕК ТЕОДОЛИТНОГО ХОДА
Точки Измеренные углы (гор) Дирекционные углы Гор прол Приращения коорд Координаты № точек
Стояния Визиров Град Мин Сек Град Мин Сек Вычисленные
Уравненные
 Х  У  Х  У
T4
T12 51 12 31 37886,284 34831,923 T12
T4 1 -0,003 0,002
T12 171 43 45 42 56 17 441,325 323,090 300,634 38209,371 35132,559 11
11 171 43 46 323,087 300,636
T12 1 -0,003 0,002
11 193 18 53 56 15 11 395,109 219,493 328,533 38428,862 35461,094 10
10 193 18 54 219,491 328,535
11 1 -0,002 0,002
10 187 32 18 63 47 30 312,470 137,998 280,346 38566,858 35741,442 9
9 187 32 19 137,996 280,348
10 1 -0,003 0,002
9 200 53 34 84 41 5 446,753 41,385 444,832 38608,240 36186,276 8
8 200 53 35 41,382 444,834
9 1 -0,003 0,002
8 167 10 9 71 51 15 397,031 123,650 377,285 38731,887 36563,564 7
7 167 10 10 123,647 377,287
8 1 -0,002 0,002
7 158 48 35 50 39 51 308,962 195,840 238,965 38927,725 36802,530 6
6 158 48 36 195,838 238,966
7 0 -0,002 0,002
6 218 51 37 89 31 28 346,434 2,875 346,422 38930,598 37148,954 13
13 218 51 37 2,873 346,424
6 1 -0,004 0,003
13 192 48 18 102 19 47 523,302 -111,744 511,232 38818,851 37660,189 14
14 192 48 19 -111,748 511,235
13 0 -0,004 0,003
14 152 47 41 75 7 28 527,923 135,529 510,230 38954,376 38170,422 15
15 152 47 41 135,525 510,233
14 1 -0,002 0,002
15 174 48 35 69 56 4 357,996 122,827 336,266 39077,200 38506,689 16
16 174 48 36 122,824 336,268
15 0 -0,002 0,002
16 184 41 52 74 37 56 313,561 83,098 302,349 39160,296 38809,040 17
17 184 41 52 83,096 302,351
16 1 -0,002 0,002
17 190 22 31 85 0 28 302,092 26,288 300,946 39186,582 39109,988 T18
T18 190 22 32 26,286 300,948 39186,582 39109,988
17 0
T18 185 11 30 90 11 58
T19 185 11 30

[Х ф] [Yф]

 1300,329 4278,041
P 4672,958

[Х т] [Y т]

 1300,298 4278,065

f β

 -9

f x f y

 0,031 -0,024

f l

 0,040

f l/P

 0,000008
допуск 0,000100
поправка -0,003

ПРИЛОЖЕНИЕ В

В Е Д О М О С Т Ь
ХОД № 1
ВЫЧИСЛЕНИЯ КООРДИНАТ ТОЧЕК ТЕОДОЛИТНОГО ХОДА
Точки Измеренные углы (гор) Дирекционные углы Гор прол Приращения коорд Координаты № точек
Стояния Визиров Град Мин Сек Град Мин Сек Вычисленные
Уравненные
 Х  У  Х  У
T2
T01 138 27 9 40693,570 36113,380 T01
T2 2 0,002 0,007
T01 167 43 48 126 10 59 363,080 -214,350 293,055 40479,221 36406,441 2
2 167 43 50 -214,349 293,061
T01 1 0,002 0,008
2 214 12 1 160 23 1 442,312 -416,641 148,493 40062,583 36554,943 3
3 214 12 2 -416,639 148,502
2 2 0,002 0,007
3 201 10 36 181 33 39 346,536 -346,407 -9,439 39716,177 36545,511 4
4 201 10 38 -346,406 -9,432
3 1 0,002 0,008
4 176 36 11 178 9 51 403,438 -403,231 12,924 39312,948 36558,443 5
5 176 36 12 -403,229 12,932
4 2 0,002 0,009
5 149 28 57 147 38 50 456,024 -385,235 244,032 38927,715 36802,484 6
6 149 28 59 -385,233 244,041 38927,715 36802,484
5 1
6 92 46 15 60 25 6
6a 92 46 16

[Х ф] [Yф]

 -1765,865 689,066
P 2011,390

[Х т] [Y т]

 -1765,855 689,104

f β

 -9

f x f y

 -0,010 -0,038

f l

 0,039

f l/P

 0,000020
допуск 0,000100
поправка 0,001

ПРИЛОЖЕНИЕ Г

В Е Д О М О С Т Ь
ХОД № 2
ВЫЧИСЛЕНИЯ КООРДИНАТ ТОЧЕК ТЕОДОЛИТНОГО ХОДА
Точки Измеренные углы (гор) Дирекционные углы Гор прол Приращения коорд Координаты № точек
Стояния Визиров Град Мин Сек Град Мин Сек Вычисленные
Уравненные
 Х  У  Х  У
T4
T12 51 12 31 37886,284 34831,923 T12
T4 0 -0,013 -0,001
T12 171 43 45 42 56 16 441,325 323,091 300,632 38209,362 35132,554 11
11 171 43 45 323,078 300,631
T12 0 -0,012 -0,001
11 193 18 52 56 15 8 395,109 219,498 328,530 38428,849 35461,083 10
10 193 18 52 219,486 328,529
11 0 -0,009 -0,001
10 187 32 17 63 47 25 312,470 138,005 280,343 38566,845 35741,425 9
9 187 32 17 137,996 280,342
10 0 -0,013 -0,001
9 200 53 34 84 40 59 446,753 41,398 444,831 38608,230 36186,255 8
8 200 53 34 41,385 444,830
9 1 -0,012 -0,001
8 167 10 8 71 51 8 397,031 123,663 377,281 38731,881 36563,535 7
7 167 10 9 123,651 377,280
8 0 -0,009 -0,001
7 158 48 35 50 39 43 308,952 195,843 238,949 38927,715 36802,484 6
6 158 48 35 195,834 238,949 38927,715 36802,484
7 1
6 189 45 22 60 25 6
6a 189 45 23

[Х ф] [Yф]

 1041,499 1970,566
P 2301,640

[Х т] [Y т]

 1041,431 1970,561

f β

 -2

f x f y

 0,068 0,005

f l

 0,068

f l/P

 0,000029
допуск 0,000100
поправка -0,006

ПРИЛОЖЕНИЕ Д

В Е Д О М О С Т Ь
ХОД № 3
ВЫЧИСЛЕНИЯ КООРДИНАТ ТОЧЕК ТЕОДОЛИТНОГО ХОДА
Точки Измеренные углы (гор) Дирекционные углы Гор прол Приращения коорд Координаты № точек
Стояния Визиров Град Мин Сек Град Мин Сек Вычисленные
Уравненные
 Х  У  Х  У
T19
T18 270 11 58 39186,582 39109,988 T18
T19 -2 0,007 -0,005
T18 174 48 30 265 0 26 302,092 -26,291 -300,946 39160,298 38809,037 17
17 174 48 28 -26,284 -300,951
T18 -2 0,007 -0,005
17 16 169 37 29 254 37 53 313,581 -83,108 -302,368 39077,198 38506,664 16
169 37 27 -83,100 -302,373
17 -1 0,008 -0,006
16 175 18 9 249 56 1 357,998 -122,832 -336,266 38954,374 38170,392 15
15 175 18 8 -122,824 -336,272
16 -2 0,012 -0,009
15 185 11 25 255 7 24 527,923 -135,539 -510,227 38818,848 37660,156 14
14 185 11 23 -135,526 -510,236
15 -1 0,012 -0,009
14 207 12 19 282 19 42 523,302 111,732 -511,235 38930,592 37148,912 13
13 207 12 18 111,744 -511,244
14 -2 0,008 -0,006
13 167 11 42 269 31 22 346,434 -2,885 -346,422 38927,715 36802,484 6
6 167 11 40 -2,877 -346,428 38927,715 36802,484
13 -1
6 330 53 45 60 25 6
6a 330 53 44

[Х ф] [Yф]

 -258,923 -2307,463
P 2371,330

[Х т] [Y т]

 -258,867 -2307,504

f β

 11

f x f y

 -0,056 0,041

f l

 0,069

f l/P

 0,000029
допуск 0,000100
поправка 0,005
© 2011 Рефераты и курсовые работы